h
ما هو لغز عـدد برنـولي؛
Jacob Bernoulli
تمكن فتى مهاجر عراقي في السادسة عشرة من العمر يقيم في السويد، من فك أحجية رياضيات شغلت الخبراء لأكثر من 300 عام في غضون أربعة شهور فقط، بحسب ما ذكرت صحيفة «داغينز نيهيتر»السويدية أمس. حيث وجد محمد التميمي صيغةً لتفسير وتبسيط الأحجية المسماة «عدد برنولي» وهي سلسلة من الحسابات سميت تيمناً بعالم الرياضيات السويسري جاكوب برنولي (Jacob Bernoulli) الذي عاش في القرن السابع عشر.
وقال الصبي العراقي الذي أتى إلى السويد مع والديه قبل ستة أعوام، لصحيفة «فالو كوريرين Falu Kuriren» وهو في الصف الاول الثانوي إن المعلمين في مدرسة مدينته فالون «لم يقتنعوا بادئ الأمر» بعمله، مضيفاً أنه اتصل بالاستاذ Lars-Ake Lindahl في جامعة أوپسالا، إحدى اعرق الجامعات السويدية، ليطلب منه التدقيق في عمله. وبعد تفحص دفاتره وجد الاستاذ أنه فك بالفعل الأحجية وعرض عليه الانضمام إلى الجامعة، لكنه رفض مفضلاً التركيز على دراسته وتلقي دروس مكثفة في الرياضيات خلال فصل الصيف. وذكر الفتى العراقي أنه يتمنى أن يكون «باحثاً في الفيزياء أو الرياضيات»، مستطرداً بالقول إن عليه أن يحسن من لغته الانگليزية والعلوم الاجتماعية.
----===--------===-----
----===--------===-----
أعداد برنولي Bernoulli numbers ، هي متتالية من الأعداد الكسرية ذات علاقة وثيقة مع نظرية الأعداد، ويرتبطون بقيم اقتران ريمان الزائي للأرقام الصحيحة السالبة.
من حيث التعريف فإن عدد برنولي هو صيغة رياضية كسرية لتتابع الارقام المنطقية ذات الصلة بنظرية الارقام وهي مرتبطة بدالة زيته (التي وضعها العالم الالماني ريمان) بعدد صحيح سالب. إن نظرية الارقام هي فرع من الرياضيات البحتة ويدرس الارقام بصورة عامة ويركز على الارقام الصحيحة والتمارين الرياضية المتعلقة بها. أما دالة زيته (التي وضعها العالم الالماني ريمان) فهي دالة رياضية معروفة في علم الرياضيات وذلك بسبب تأثيرها المباشر على توزيع الارقام الاولية بالاضافة الى أهمية هذه الدالة في الفيزياء ونظرية الاحتمالات والاحصاء التطبيقي. ان نظرية ريمان ( التي تتعامل مع توزيع الاصفار في الدالة ) تعتبر عند الكثير من علماء الرياضيات ومنذ عام 1732 من المسائل الرياضية غير القابلة للحل.
ولکن يبدو ان ارض السويد هي منبع الافكار الرياضية لانه كان هناك عالم للرياضيات إسمه Marcel Riesz من المجـرقد هاجر للسويد واستقر في جامعة لوند الواقعة شمال مالمو قد حاول في عام 1916 ان يحل المعادلة، وهو أخ عالم الرياضيات المشهور Frigyes Riesz. وبرغم ان Marcel Riesz قد إقترب من الحل إلا إنه لم يتمكن من تحديد قيمة عددية لرقم برنولي أو حتى قيمة دالية من أي قطع كانت حتى لو خطية.
ترتكز دالة زيتا التي جاء بها برنولي على مجموع عددي لمعادلة عددية من الدرجة ( n ) يكون فيها المعامل العام هو ( m ) كما في المعادلة التالية؛ حيث تتراواح قيمة معامل التجميع ( k ) من صفر الى ( m-1 ):
في حيم إن نفس المجموع العددي يعطي القيمة التالية:
وهنا ظهر عدد برنولي ( B ) واضحا ً للاساس ( k ) الذي هو نفسه قيمة عددية لمجموع الدالة. وكمثال على ذلك؛ فإنه لو أن المعامل ( n ) أخذ القيمة 1 فان:
لم يتمكن عالم الرياضيات لحد وفاته في عام 1969 عن عمر ناهز 82 سنة من إيجاد معالجة رياضية سواء عددية كانت أو منطقية من فك معادلته التي إقترحها للوصول إلى حل يؤدي لوضع قيمة دالية أو عددية لرقم برنولي، حيث انه وضع هذه الدالة التالية لتقوده لفك طلاسم رقم برنولي:
توقف العقل البشري عن وضع حل للمعادلة الرياضية منذ آخر محاولة في 1916 وتم إعتبارها غير قابلة للحل أو على الاقل لايوجد حل!!! مثلما يتم قسمة أي عدد صحيح على صفر؛ حيث لايوجد قيمة للناتج لانه سلسلة من الارقام التي لاتنتهي
وبقي الحال كما هو حتى جاء فتى الرافدين محمد التميمي ليتمكن من وضع حل ذو معنى رياضي لرقم برنولي وفك اللغز.





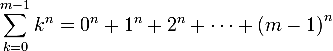
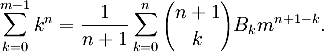
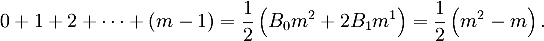
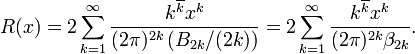
 رد مع اقتباس
رد مع اقتباس