ما هو حجم اللانهاية؟ أقصر إجابة هي أن ∞ (رمز اللانهاية) كبير جدا. بحيث لو تخيلنا ان خطًا مستقيمًا تمتد على طوله اعداد كبيرة, فان لكل عدد كبير عملاق موجود على ذلك الخط ، على سبيل المثال 1000 ^1000 ، هناك عدد اخر اكبر منه ، أي 1000^1000 + 1. الاعداد التي تستمر الى ما لا نهاية هي الفكرة التقليدية وراء مصطلح (اللا نهائي), ومع ذلك فان الرياضيين يتعاملون مع هذا المصطلح بطرق مختلفة.
عالم الرياضيات الالماني جورج كانتور ( Georg Cantor) قدم لنا مفهوما مختلفا لمصطلح اللا نهاية, في نفس الوقت الذي وضع فيه نظرية كانت لها الاثر الكبير على الرياضيات الحديثة. تقوم نظرية كانتور على مفاهيم حسابية بدائية غالبا ما نستخدمها في الحياة اليومية.
لنفترض ان هناك راعيا لا يجيد التعامل مع الارقام وحسابها, فكيف له ان يعرف كم من الخرفان لديه؟ بكل بساطة فان ذلك الراعي وعندما يطلق اغنامه للرعي في الصباح الباكر فانه سيطلع على العدد الذي يعود منها الى الحظيرة في نهاية اليوم عن طريق استخدام الحجارة. بمعنى انه في الصباح يضع في الحظيرة حجرا مقابل كل خروف يذهب الى المرعى واذا عادت الاغنام ازال تلك الاحجار. فاذا بقي من الاحجار فاضئا فان ذلك يعني ان بعض الاغنام لم ترجع مع سائر القطيع. فحتى لو يستخدم الارقام فان ذلك الراعي بارع في الرياضيات. فهو يجيد استخدام مبدأ التعويض ومبدأ التطابق (واحد مقابل واحد) للعلاقة بين اغنامه وبين الحجارة. وهذه الفكرة البدائية لها بعض النتائج المدهشة.
نظرية كانتور تشمل ايضا المجموعات التي تتألف من العناصر. مثلا N= {1,2,3,4,5,6,7,8...} تعني انها لمجموعة اعداد صحيحة وموجبة. وبالطبع فاننا يمكن ان نقسم الى تلك المجموعة الى مجموعات اصغر. مثلا:
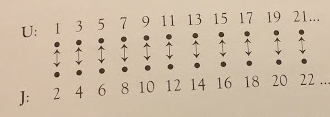
U= { 1,3,5,7...} و J= { 2,4,6,8...} فان كلا من U و J مجموعتان للاعداد الفردية والاعداد الزوجية.
واذا ما واجهنا هذا السؤال: هل كمية الاعداد الزوجية هي نفسها كمية الاعداد الفردية؟ فان جوابنا سيكون بنعم, حتى لو لم نقم بعدّ الاعداد الفردية ولا الزوجية في كل مجموعة ومقارنتها مع الاخرى. فكيف اذن نتأكد من صحة الجواب؟ في الواقع ان جوابنا مبني على الاعتقاد بان ( نصف الاعداد الموجبة الصحيحة زوجي ونصفها الاخر فردي). وحتى كانتور سيوفقنا على صحة الجواب ولكن لسبب اخر:
فهو سيقول اننا في كل مرة نحصل على فردي سيكون لدينا بجانبه ايضا عدد زوجي اخر. اي ان فكرته بان المجموعتين U و J لديهما نفس كمية العناصر مبنية على اساس ربط كل عنصر فردي من مجموعة مع عنصر زوجي من مجموعة اخرى.
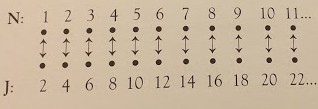
سؤال اخر: هل كمية الاعداد الصحيحة هي نفسها كمية الاعداد الفردية؟ الجواب: كلا, فان عدد عناصر المجموعة N هو ضعف عدد عناصر المجموعة U.
ومع ذلك ، فإن مصطلح "أكثر" غير واضح تمامًا عندما يتعلق الأمر بمجموعات عدد عناصرها غير محدد . فنحن نصل الى النتائج بشكل أفضل مع فكرة المطابقة واحدة مقابل واحد. المثير للدهشة ، هناك ايضا تطابق واحد مقابل واحد بين N ومجموعة الاعداد الزوجية J.
وهنا نصل الى استنتاج مذهب وهو ( ان مجموع عناصر الاعداد الصحيحة هو نفسه مجموع عناصر الاعداد الزوجية) هذا يجعلنا في مواجهة مع علماء الاغريق القدماء. ففي بداية كتاب ( العناصر) ذكر اقليدس (الكل دائما اكبر من الجزء).
يُطلق على كمية الاعداد في المجوعة الواحدة مصطلح الاصلية او الكردينالية (Cardinality). فمثلا كردينالية المجموعة {a,b,c,d,e} تساوي خمسة, والتي يمكن ان تُكتب بصيغة:
card{a,b,c,d,e}=5
واما كردينالية الاعداد الصحيحة N وكل مجموعة تتطابق مع N على اساس مبدأ واحد مقابل واحد فقد استخدم كانتور الحرف الف من اللغة العبرية (א ) للتعبير عن تلك العلاقة. وبطريقة رياضية فانها تُكتب:
card(N)=card(U)=card(J)= א
على ان كل مجموعة تدخل في العملية الحسابية اعلاه وتتطابق وفق واحد مقابل واحد مع N تسمى (مجموعة لا متناهية قابلة للعد), ويعني ذلك اننا يمكن ان ندوّن كل العناصر في تلك المجموعة بقائمة. فالقائمة بالاعداد الفردية على سبيل المثال يمكن ان تكون 1,3,5,7... ونحن على علم باي عنصر يأتي اولا ثم التالي والثالث وهكذا.
مجموعة الاعداد الكسرية Q اكبر من مجموعة الاعداد الطبيعية N. فهل يمكن ان ندوّن جميع عناصر Q في قائمة؟ فهل يمكننا توفير قائمة بحيث كل الاعداد الكسرية, حتى السالبة منها, تجد لها مكانا في تلك القائمة؟ يبدو ان فكرة تطابق واحد مقابل واحد مع المجموعة N مستحيلة.
الا اننا ببعض الحيل يمكن التغلب على تلك الاستحالة. فمثلا يمكننا ان نفترض وجود لوح ثنائي الابعاد لتدوين الاعداد. في اعلى ذلك اللوح نبدأ اولا بتدوين صف بكل الاعداد الطبيعية, سواء الموجبة او السالبة. ثم في الصف التالي ندوّن الاعداد الكسرية ذات المقام 2, على ان نقوم بحذف الكسور التي يكون لها نفس قيمة العدد في الصف الاول مثل (6/2=3 او 2/2=1). ثم في الصف الثالث ندوّن الكسور ذات المقام 3, وايضا نحذف منها الكسور التي لها نفس قيمة العدد في الصف السابق. وهكذا نستمر بالتدوين على هذا المنوال.
بالطبع سوف لن نتمكن من تدوين كل الكسور, الا اننا على الاقل اصحبنا على علم بموضع كل كسر في المخطط الذي رسمناه. فمثلا الكسر الكسر ( 209/67) يمكن ان نجده في الصف 67, تقريبا يقع بعد 200 عدد من يمين الكسر (1/67).
من خلال إظهار الكسر بهذه الطريقة ، يمكننا ، من الناحية النظرية على الأقل ، بناء قائمة أحادية البعد.إذا بدأنا في الصف العلوي وانتقلنا تدريجيا إلى اليمين ، فاننا فلن نصل إلى الصف الثاني.ولكن من خلال اختيار مسار متعرج يمكن لنا أن ننجح. لتكن البداية مع الرقم 1: 1,1-, 1/2, 1/3, 1/2-, 2, 2-...وهكذا بحسب ما تشير الاسهم. فان كل كسر سواء كان موجبا او سالبا لابد ان يكون له مكانا في القائمة الخطية. وعليه فاننا نستنتج ان مجموعة الاعداد الكسرية (ََQ) هي مجموعة لا متناهية قابلة للعد, وعليه فان:
card(Q)=א
على الرغم من أن قائمة الكسور على خط الاعداد تحتوي على العديد من العناصر التي هي بالواقع اعداد حقيقية ، فهناك أيضاً أرقام حقيقية مثل الجذر التربيعي للعدد 2 و العدد e ولكنها ليست كسورا. هذه الاعداد غير النسبية تملأ الفجوات حتى نحصل على خط رقمي بالأرقام الحقيقية R.
تلك الفجوات المعبأة بالاعداد غير النسبية تشير الى ان R سلسلة متصلة من الاعداد. ولكن كيف لنا ان نحصل على قائمة بالاعداد الحقيقية؟
من خلال حركة رائعة اثبت لنا كانتور ان محاولة حصر الاعداد التي تقع بين 0 و 1 في قائمة سيكون مصيرها الفشل. كان ذلك بمثابة صدمة لكل اولئك الذين يحبون وضع القوائم ، وتسائلوا مع انفسهم لماذا لا يمكن كتابة مجموعة متنوعة من الاعداد الواحد تلو الآخر؟
لنفترض انك لا تتفق مع كانتور في رأيه, وانت تعلم ان كل عدد بين 0 و 1 يمكن ان نعبر عنه بصف طويل من الاعداد العشرية. فمثلا 1/2=0,5000000000...الخ
و ط/1=0,31830988618379...الخ. وحينها تقدمها الى كارنتور على انها قائمة بالاعداد بين 0 و1, ولنسميها:
r1,r2,r3,,r4...الخ.
لنقم بتحليل تلك القائمة, وتسليط الضوء على بعض الاعداد فيها لتشكل وترا:
r1: 0,a1,a2,a3,a4,a5
r2: 0,b1,b2,b3,b4,b5
r3: 0,c1,c2,c3,c4,c5
r5: 0,d1,d2,d3,d4,d5
ولكن اين العدد x= 0,x1,x2,x3,x4,x5 ؟ حيث تختلف:
x1 عن a1 و x2 عن b2 و x3 عن c3 و x4 عن d4
وهكذا كلما واصلنا المسير مع خط الوتر! اذن x تختلف عن كل عدد في القائمة التي انشئناها من الاعداد العشرية, وعليه فان افتراض كانتور كان صحيحا!
في الواقع ، لا توجد قائمة ممكنة لمجموعة الأعداد الحقيقية R ، لذا فهي عبارة عن (اكبر) مجموعة لا متناهية ،اي انها ذات تصنيف اعلى من مجموعة الاعداد الكسرية Q. فالكبير اصبح الان اكبر!







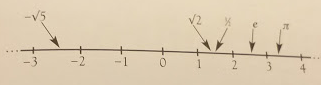
 رد مع اقتباس
رد مع اقتباس

 ونتأكد انو عدد U يساوي عدد J
ونتأكد انو عدد U يساوي عدد J

