المربع السحري هو عبارة عن مربع مكون من خانات تحتوي على اعداد غير مكررة, حاصل جمع تلك الاعداد هو نفسه سواء للاعمدة اوالصفوف اوالاقطار.
ونتيجة لذلك لا يمكن اعتبار المربع المكون من خانتين افقيا وعموديا (2x2) مربعا سحريا, باعتبار ان احد الاعداد سيكون مكررا والا لن تكون نتيجة الجمع واحدة في كل الاتجاهات. وكمثال لنفترض توزيع الاعداد كما في الشكل التالي:

فذلك يعني ان:
a+
b=a+
c
وبالتالي:
b=c
ولكن ماذا عن مربع 3x3؟
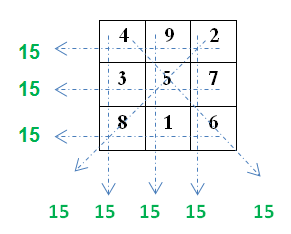
لنرسم مربعا مقسم الى 9 خانات, في كل خانة احد الاعداد من 1 الى 9. ولكن قبل ذلك علينا ان لا ننسى ان مجموعة الاعداد من 1 الى 9 يساوي 45, مما يعني ان حاصل جمع الاعداد في كل ثلاث خانات في اتجاه معين يجب ان يكون 15.
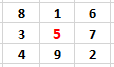
ولنطلق على خانة الوسط الرمز Z, فان Z تتقاطع في خط عمودي واخر افقي وخطين قطرين:
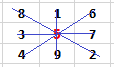
فاذا ما قمنا بجمع كل تلك الخطوط التي تتقاطع مع Z فاننا نحصل على:
15+15+15+15=60
وهذا الناتج يجب ان يكون مساويا لعملية جمع ناتج كل الاعداد (45) مع (Z) المضروبة في 3:
45+3Z=60
ويعني ان
Z=5.
امر اخر علينا ملاحظته: لا يمكن ان نضع العدد 1 في احدى الخانات باحدى الزوايا.
والان بعد حصولنا على كل المعلومات المطلوبة ليس علينا الا نقوم بالتجربة.
ومنذ ان عرف المربع السحري كان الانسان دؤوبا على وضع الية تسهّل عملية تصميم مربعا سحريا. واحدى تلك الاليات الفعالة كانت من ابتكارات السفير الفرنسي في تايلاند القديمة, في نهاية القرن السابع عشر, سيمون دي لا لوبرا ( Simon de la Loubera) والذي كان مهتما باساليب العدّ الصيني.
وكانت الالية التي وضعها قائمة على اساس :
1. ان يكون عدد الخلايا في المربع سحري عددا فرديا,
2. وان يُوضع العدد واحد في مربع الوسط من العمود الافقي الاول او الاخير,
3. ومن ثم توزيع الاعداد الاخرى بشكل عشوائي:

وللعلم فان هذا المربع مشهور لدى الصينيين منذ 3000 سنة قبل الميلاد, ويطلق عليه اسم
مربع لوشو ( Lo Shu Square). وبحسب الاسطورة فان هذا المربع منحته الالهة للصينيين انذاك وكان مرسوما على قوقعة سلحفاة خرجت من نهر لو. وتم اعتباره حينها انه رسالة من الالهة تطلب فيها زيادة القرابين لتخليص البشر من الطاعون.
ولكن الامر الغريب انه لا يوجد الكثير من المربعات السحرية المؤلفة من ثلاث اعمدة وثلاث صفوف.
ولكن ماذا عند مربع 4x4؟ فهل تعلم انه يوجد 880 مربعا سحريا؟ وهل تصدق انه يوجد 2202441792 مربعا سحريا من نوع 5x5؟ ولكَ ان تتخيل عدد المربعات السحرية من نوع nxn!
واذا كان مربع شولو السحري قد اصبح مشهورا فانه بسبب عمر اكتشافه, ولانه من المدهش ان يتم اكتشافه قبل خمسة الاف عام. في حين ان المربع السحري 4x4 اصبح رمزا بسبب ارتباطه باحد اشهر فناني عصر النهضة, اضافة الى خصائصه التي جعلت منه بمئات النسخ المختلفة.
ففي عام 1514 قام الرسام الالماني الشهير البرخت دورر (Albrecht Dürer) برسم لوحة تعكس الواقع الكئيب للمجتمع البشري اطلق عليها اسم
ميلينكوليا 1 (1 Melankólia ), ما يميز هذه اللوحة انها تحتوي على نقش لمربع سحري.


ان مربع الكابة هذا ـ كما يُطلق عليه ـ يحتوي على العديد من الرموز والاسرار, من بينها ان حاصل جمع كل من اعمدته وصفوفه الاربعة وخطيه القطرين الرئيسين يساوي 34. كذلك في وسط الصف السفلي من المربع يوجد تسلسل عددي (15 و 14) في اشارة الى العام الذي رُسمت فيه اللوحة.
احد الرموز التي لمعت ايضا في عالم تصميم المربعات السحرية, هو العالم الامريكي ورجل الدولة الشهير بنجامين فرانكلين (Bemjamin Franklin), فقد كان يرى ان تصميم المربعات السحرية وسيلة جيدة لشحذ ذاكرته. وحتى اليوم لم يفهم علماء الرياضيات كيف كان صمم فرانكلين ـ بعبقرية مذهلة ـ مربعات سحرية كبيرة ومعقدة, مع ان فرانكلين اقر انه كان يستهلك الكثير من الوقت في شبابه فقط في محاولات لتصميم مربعات سحرية.
واذا ما سلطنا الضوء على احد تلك المربعات التي صممها فرانكلين, وهو مربع من فئة 8x8, فلا نبالغ ان قلنا انه يستحق ان يكون احد عجائب الدنيا التي ابتكرها البشر.
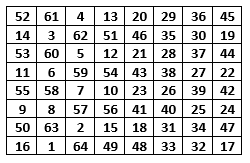 من الاسرار المدهشة لهذا المربع:
من الاسرار المدهشة لهذا المربع:
1. ان حاصل جمع كل من اعمدته وصفوفه الثمانية وخطيه القطرين الرئيسين يساوي 260
2. ان حاصل جمع كل تدرج من احدى الزوايا حتى مربعي الوسط ثم الصعود نحو الزاوية الاخرى يساوي 260, كما في الشكل

3. حاصل جمع كل مربع من فئة 2x2 يساوي ايضا 130, وكذلك حاصل جمع الزوايا ايضا يساوي نفس النتيجة.
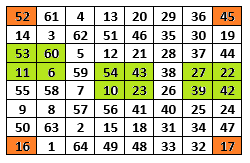
4. ان حاصل جمع كل نصف سطر افقي او عمودي يساوي 130:
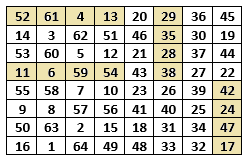
واذا ما بحثت اكثر فقد تكتسف اسرار اخرى لهذا المربع العجيب.
يمكن لبعض المربعات السحرية ان تكون مؤلفة من خانات تحتوي على اعداد تربيعية, وقد كان للفرنسي ادوارد لوكاس (Edouard Lucas) احد علماء الرياضيات في القرن التاسع عشر, كان له افضلية السبق في تصميم بعض تلك المربعات. ولكن حتى يومنا الحاضر لم يتمكن اي عالم رياضي او شخص اخر من ايجاد مربع سحري واحد من فئة 3x3 تحتوي خاناته على اعداد تربيعية, بالرغم من ان احد المربعات كان قريبا جدا من ان يكون سحريا:

فان مجموع كل عمود من اعمدته وصف من صفوفه الثلاثة واحد قطريه يساوي 21629, في حين ان الخط القطري الاخر ـ الملون باللون الاصفر في الشكل السابق ـ يشذ عن القاعدة ليساوي مجموع ارقام خاناته 38307. واذا كان لديه الطموح والحماس لايجاد احد تلك المربعات فعليك ان تتذكر ان معدل مجموع كل الخانات يجب ان يكون اكبر من 2.5*10^2 لذلك لا داعي لان تضيع وقتك بفحص الاعداد الصغيرة.
واذا كانت مبرهنة فيرما الاخيرة قد تم اثباتها باستخدام المنحنيات الاهليجية, فانه بنفس المنحيات قد تم البرهان على عدم وجود مربع سحري من فئة 3x3 يحتوي على اعداد تكعيبية او اكبر.
ومع ذلك, فان البحث عن المربعات ذي الاعداد التربيعية كان ناجحا بالنسبة للمربعات الاكبر من 3x3, حيث تم ايجاد مربعات 4x4 و 5x5. ففي عام 1770 وضع السويسري ليونهارت اويلر (Leonhard Euler ) مثالا لاحد تلك المربعات, دون ان يذكر الالية التي صمم على اساسها ذلك المربع.
ان المربعات السحرية الكبرى لديها خصائص مذهلة. فالمربع 32x32 الذي تم تصميمه من قِبَل الخبير في هذا المجال الامريكي وليام بنسون (William H. Benson) يمكن ان يحتوي على اعداد تربيعية او تكعيبية. وعام 2001 تم تصميم مربع عملاق, 1024x1024, يمكن لجميع اعداده حتى الاس من الدرجة الخامسة ان تجعل منه مربعا سحريا.
يمككنا انشاء العديد من المربعات السحرية اذا ما تنازلنا عن بعض الشروط. فلو الغينا شرط ان يكون حاصل جمع الاقطار هو نفسه حاصل جمع الاعمدة والصفوف, فان ذلك سيعطينا وفرة من النتائج المذهلة. وحينها سنتمكن من البحث مثلا عن انشاء مربعات سحرية مكونة فقط من الارقام الاولية.
واذا كانت هناك جائزة تُمنح فانها يجب ان تكون من نصيب المهندس الهولندي لي سالوس (Lee Sallows) الذي استطاع تصميم المربع 3x3 التالي:
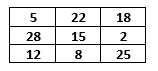 لكن ما الذي يميز هذا المربع؟
لكن ما الذي يميز هذا المربع؟
لنعيد كتابة الاعداد بالحروف وباللغة الانكليزية:
| eighteen |
twenty two |
five |
| two |
fifteen |
twenty eight |
| twenty five |
eight |
twelve |
والان لنجمع عدد الحروف في كل خانة:
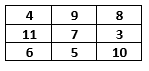
نعم, اننا نرى مربعا سحريا اخر!! واذا ما ركزنا اكثر يمكننا ان نلاحظ ان هذا المربع يحتوي على اعداد متعاقبة من الـ 4 الى الـ 11. وليس هذا فحسب, اذ ان العدد السحري للمربع الاول هو 45 في حين 21 هو العدد السحري للمربع الثاني, وكلا العددين من مضاعفات الـ 9 (3x3=9)!
مواضيع قد تهمك:
-
مبرهنة فيرما الاخيرة
-
الاعداد الاولية






 المربع السحري في الرياضيات
المربع السحري في الرياضيات














 رد مع اقتباس
رد مع اقتباس




 وباقي الموضوع تاريخ تقريبا
وباقي الموضوع تاريخ تقريبا