دوال مثلثية
رياضيات
ميّز عن دالة مثلثية الشكل.
في الرياضيات، الدوال المثلثية أو التوابع المثلثية(بالإنجليزية: Trigonometric Functions) هيدوال لزاوية هندسية.[1][2][3] وهي دوال مهمة عندما يُراد دراسة مثلث أوعرض ظواهرِ دورية أو متكررة كالموجات. يمكن تعريف هذه الدوال نسبةً بين أضلاع مثلث قائم يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية إحداثياتٍ على دائرة مثلثيةأو دائرة واحدية. يعتبر دوما عند الإشارة إلى المثلثات أن الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي)، وذلك ليكون مجموع الزوايا 180 درجة دائما.
الدوال المثلثية الأكثر انتشارا هي دالة الجيب (يرمز إليها ب Sin) ودالة الجيب التمام (يرمز إليها ب Cos) ودالة الظل (يرمز إليها ب Tg أو Tan).
التعريف باستعمال المثلث قائم الزاويةعدل
توجد ثلاثة دوال مثلثية أساسية هي:
- الجيب، ويساوي النسبة بين الضلع المقابل للزاوية مقسوما على الوتر.
- جيب التمام، ويساوي النسبة بين الضلع المجاور للزاوية مقسوما على الوتر.
- الظل، ويساوي النسبية بين الضلع المقابل للزاوية والضلع المجاور لها.
جيب زاوية والجيب التمام لزاوية وظل زاويةعدل
الاسم الترميز العربي الترميز اللاتيني العلاقة الرياضياتية جيب جا sin {\displaystyle \sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)\,} جيب تمام جتا cos {\displaystyle \cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)\,} ظل ظا tan {\displaystyle \tan \theta ={\frac {1}{\cot \theta }}={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)\,} ظل تمام ظتا cot {\displaystyle \cot \theta ={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)\,} قاطع قا sec {\displaystyle \sec \theta ={\frac {1}{\cos \theta }}=\csc \left({\frac {\pi }{2}}-\theta \right)\,} قاطع تمام قتا csc {\displaystyle \csc \theta ={\frac {1}{\sin \theta }}=\sec \left({\frac {\pi }{2}}-\theta \right)\,}
التعريف باستعمال دائرة الوحدةعدل
دائرة الوحدة
يمكن أن تعرف الدوال المثلثية الستة بواسطة دائرة الوحدة(دائرة شعاعها يساوي الواحد ومركزها هو أصل المَعلم).
يمكن هذا التعريف من تعريف الدوال المثلثية بالنسبة لجميع الأعداد الموجبة والسالبة وليس فقط الأعداد المحصورة بين الصفر وπ/2 راديان.
التعريف باستعمال المتسلسلاتعدل
دالة الجيب (باللون الأزرق) تحسب بصفة تقريبية اقترابا كبيرا بواسطةمتعددة الحدود لتايلور من الدرجة السابعة (باللون الوردي) بالنسبة لدورة كاملة متمركزة حول أصل المَعلم.
الدوال المثلثية هي دوال تحليلية. يمكن تمثيل جميع الدوال المثلثية بواسطة متسلسة تايلور كالتالي:
الزاوية x مقاسة بالتقدير الدائري في جميع السلاسل التالية
جيب الزاوية:
{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\[8pt]\end{aligned}}}
جيب تمام الزاوية:
{\displaystyle {\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}}
تعتبر هاتان الصيغتان في بعض الأحيان تعريفيت لدالتي الجيب والجيب التمام. عادة ما تُستعملان نقطة بداية في إطار التطرق القوي والدقيق إلى الدوال المثلثية (على سبيل المثال متسلسلة فورييه).
ظل الزاوية:
{\displaystyle {\begin{aligned}\tan x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}}
قاطع تمام:
{\displaystyle {\begin{aligned}\csc x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}
قاطع:
{\displaystyle {\begin{aligned}\sec x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\\&{}=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}}
ظل تمام:
{\displaystyle {\begin{aligned}\cot x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}
التقريب بالجذور
مثال :
{\displaystyle \cos {\frac {\pi }{9}}={\frac {\sqrt[{3}]{6\times {\frac {\sqrt[{3}]{6\times {\frac {\sqrt[{3}]{6\times \cdots +1}}{2}}+1}}{2}}+1}}{2}}}
العلاقة بدالة الأس وبالأعداد العقديةعدل
يمكن أن يُبين من خلال التعريفات باستعمال المتسلسلات بأن دالتي الجيب والجيب التمام هما الجزء العقدي والجزء الحقيقي على التوالي، لدالة الأس المطبقة على الأعداد العقدية، حين يكون مدخلها عددا تخيليا صرفا:
{\displaystyle e^{i\theta }=\cos \theta +i\sin \theta .\,}
تسمى هاته المتطابقة بصيغة أويلر. هكذا، تصير الدوال المثلثية مركزية وأساسية في الفهم الهندسي للتحليل العقدي.
قد تستعمل صيغة أويلر للحصول على بعض المتطابقات المثلثية، وذلك بكتابة دالتي الجيب والجيب التمام كما يلي:
{\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\;}
{\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\;}
بالإضافة إلى ذلك، يمكن هذا الأمر من تعريف الدوال المثلثية على الأعداد العقدية.
انظر إلى دالة كاملة.
التعريف بواسطة المعادلات التفاضليةعدل
كل من دالتي الجيب والجيب التمام تحققان المعادلة التفاضلية التالية:
{\displaystyle y''=-y.\,}
بتعبير آخر، كل منهما تساوي مقابل مشتقتها من الدرجة الثانية.
متطابقاتعدل
مقالة مفصلة: قائمة المطابقات المثلثية
هناك عدد من المتطابقات تربط الدوال المثلثية بعضها ببعض. تعتبر متطابقة فيتاغورس واحدة من أكثر المتطابقات انتشارا واستعمالا. تنص هاته المتطابقة على أن مجموع مربع جيب زاوية ما، ومربع الجيب التمام لهاته الزاوية يساوي واحدا.
{\displaystyle \sin ^{2}x+\cos ^{2}x=1,\,}
حيث يرمزsin2 x + cos2 x إلى sin x)2 + (cos x)2).
{\displaystyle \sin({\frac {\pi }{2}}-x)=\cos(x)}
{\displaystyle \cos({\frac {\pi }{2}}-x)=\sin(x)}
{\displaystyle \cos(\pi -x)=\cos({\frac {\pi }{2}}-(x-{\frac {\pi }{2}}))=\sin(x-{\frac {\pi }{2}})=-\sin({\frac {\pi }{2}}-x)=-\cos(x)}
{\displaystyle \sin(\pi -x)=\sin({\frac {\pi }{2}}-(x-{\frac {\pi }{2}}))=\cos(x-{\frac {\pi }{2}})=\cos({\frac {\pi }{2}}-x)=\sin(x)}
الحسابعدل
مقالة مفصلة: توليد الجداول المثلثية
حساب قيم الدوال المثلثية موضوع صعب ومعقد.
الدوال العكسيةعدل
مقالة مفصلة: الدوال المثلثية العكسية
الدوال المثلثية دورية، وبذلك، هي ليست تباينية، وبالتالي ليس لديها دالة عكسية. لهذا السبب، يصير من الضروري تقليص مجال تعريفها من أجل تعريف دالة عكسية، حتى الدوال المثلثية دوالا تقابلية.يُمكن للدوال المثلثية العكسية أن تعرف بواسطة المتسلسلات تماما كما هو الحال بالنسبة للدوال المثلثية. على سبيل المثال،
الدالة التعريف مجال التعريف {\displaystyle \arcsin x=y\,} {\displaystyle \sin y=x\,} {\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\,} {\displaystyle \arccos x=y\,} {\displaystyle \cos y=x\,} {\displaystyle 0\leq y\leq \pi \,} {\displaystyle \arctan x=y\,} {\displaystyle \tan y=x\,} {\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\,} {\displaystyle \operatorname {arccsc} x=y\,} {\displaystyle \csc y=x\,} {\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0\,} {\displaystyle \operatorname {arcsec} x=y\,} {\displaystyle \sec y=x\,} {\displaystyle 0\leq y\leq \pi ,y\neq {\frac {\pi }{2}}\,} {\displaystyle \operatorname {arccot} x=y\,} {\displaystyle \cot y=x\,} {\displaystyle 0<y<\pi \,}
{\displaystyle \arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \,.}
خصائص وتطبيقاتعدل
مقالة مفصلة: استعمالات علم المثلثات
قانون الجيبعدل
انظر إلى قانون الجيب.
منحنى ليساجو، شكل كُون باستعمال دوال تعتمد على الداوال المثلثية.
قانون الجيب التمامعدل
انظر إلى قانون جيب التمام.
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C,\,}
وقد تكتب هاته الصيغة كما يلي:
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.}
قانون الظلعدل
مقالة مفصلة: قانون الظل
قانون الظل التمامعدل
مقالة مفصلة: قانون الظل التمام
الدوال الدوريةعدل
انقر على الصورة من أجل النظر إلى صورة متحركة of the additive synthesis of a موجة مربعية with an increasing number of harmonics
الدوال المثلثية مهمة أيضا في الفيزياء. انظر إلى الحركة التوافقية البسيطة.
التاريخعدل
يمكن تتبع الدراسة في وقت مبكر من علم المثلثات إلى العصور القديمة، تم تطوير الدوال المثلثية لأنها تستخدم حتى اليوم. تم اكتشاف وظيفة الوتر (أطول ضلع من المثلث) من قبل هيبارخوس نيقية (180-125 قبل الميلاد) وبطليموس الروماني لمصر (90-165 م).
ويمكن إرجاع وظائف الجيب وجيب التمام وإلى jyā كوتي-jyā الدالات المستخدمة في الفترة غوبتا عالم الفلك الهندي (Aryabhatiya، SURYA Siddhanta)، عن طريق الترجمة من اللغة السنسكريتية إلى العربية ومن ثم من العربية إلى اللاتينية.
كانت تعرف كل ست وظائف المثلثية في الاستخدام الحالي في الرياضيات الإسلامية من القرن التاسع، كما كان قانون سينيسي ستخدم في حل المثلثات. اهتم الخوارزمي إنتاج جداول جيب التمام، وسينيس اهتم بالظلال.
أدلى مادافا من Sangamagrama (سي 1400) في وقت مبكر من خطوات تحليل الدوال المثلثية من حيث سلسلة لا نهاية لها.
نشرت أول استخدام من "الخطيئة" الاختصارات "كوس"، و"تان" هو من القرن 16 الفرنسي جيرار عالم الرياضيات ألبرت.
في ورقة نشرت في 1682، أثبت أن لايبنتز الخطيئة x هو ليس وظيفة جبري العاشر.
كان Introductio يونارد يولر في infinitorum analysin (1748) المسؤولة في الغالب لإنشاء المعاملة التحليلية للالدوال المثلثية في أوروبا، وتحديد أيضا على أنها سلسلة لا نهاية لها وتقديم "أويلر صيغة"، فضلا عن الخطيئة الاختصارات شبه الحديثة.، كوس، تانغ.، المهد، ثوانى.، ومجلس الشاحنين السنغالي. [5]
وعدد قليل من الوظائف المشتركة تاريخيا، ولكنها الآن نادرا ما تستخدم، مثل وتر (CRD (θ) == 2 الخطيئة (θ / 2))، وversine (versin (θ) = 1 - جتا (θ) = 2 sin2 (θ / 2)) (الذي ظهر في أقرب الجداول [5])، وhaversine (haversin (θ) = versin (θ) / 2 = sin2 (θ / 2))، وexsecant (exsec (θ) = ثانية (θ) - 1) وexcosecant (excsc (θ) = exsec (π / 2 - θ) == ديوان الخدمة المدنية (θ) - 1) يتم سرد العديد من العلاقات بين هذه الوظائف أكثر في المقالة حول الهويات المثلثية.
اشتقاقي، وشرط كلمة مشتقة من الكلمة السنسكريتية لوتر النصف، jya-رقصة العرضة، يختصر إلى جيفا. وقد ترجم هذا في اللغة العربية jiba، JB مكتوب، حروف العلة لا يتم كتابتها باللغة العربية. المقبل، وكان هذا سوء الترجمة ترجمة في القرن 12th إلى اللاتينية والجيوب الأنفية، تحت انطباع خاطئ بأن JB قفت لjaib الكلمة، التي تعني "حضن" أو "باي" أو "اضعاف" باللغة العربية، وكذلك الجيوب الأنفية في اللاتينية [28] وأخيرا، تحويل استخدام اللغة الإنجليزية في الجيوب الأنفية شرط أن الكلمة اللاتينية [29] الظل كلمة تأتي من اللاتينية بمعنى tangens "لمس"، منذ تلامس خط دائرة نصف قطرها وحدة، في حين ينبع من القاطع secans اللاتينية - "قطع "- منذ السطر يقطع الدائرة.
تمثيل بياني لدالة جيب التمامعدل
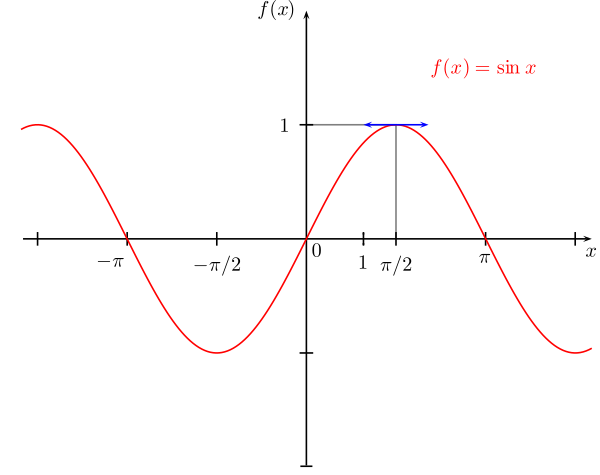
تمثيل بياني لدالة الجيبعدل
الظل التمام لزاويةعدل
صورة (1)
ظل تمام الزاوية هو النسبة بين جيب التمام والجيب لنفس الزاوية أي مقلوب ظل الزاوية. يمكن التعبير عن ظل تمام الزاوية لزاوية x -معبرا عنها بالتقدير الدائري- بواسطة سلسلة تايلور التالية:
{\displaystyle {\begin{aligned}\cot x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}
التظل هو مقلوب الظل ويساوي المجاور على المقابل. مثال:
مثلا: طول الضلع [أج] =15 سنتمتر طول الضلع [أب] =10 سنتمتر طول الضلع [ج ب] (الوتر) =19 سنتمتر لحساب تظل(cotan) الزاوية ب : المجاور [أب] / المقابل [أج] 10 / 15 = 0.66 إذن: تظل(cotan) الزاوية ب هو: 0.66





 دوال مثلثية رياضيات
دوال مثلثية رياضيات


















































 رد مع اقتباس
رد مع اقتباس