اليوم سنلتقي باصعب تحد لعلماء الرياضيات على الاطلاق واكثر فرضية تعقيدا, الى درجة انها استعصت على البرهان حتى لحظات كتابة هذا الموضوع. واذا كانت مبرهنة فيرما الاخيرة قد حالفها الحظ بعد ثلاثة قرون ونصف ـ كما ذكرنا هنا ـ وتم اعلان حل حدسية بوانكاريه بعد قرن من طرحها, فان فرضية ريمان ـ موضوعنا اليوم ـ لم تكن بهذا المستوى من النجاح, والى اليوم ما زالت مستعصية على سحر الرياضيات وادواته. فبمجرد ما يُعلن عن حلها حتى تظهر اسئلة جديدة حول توزيع الاعداد الاولية وامور اخرى تجعل الرياضيين في حيرة من امرهم.
تبدأ القصة مع جمع بعض الكسور, مثل:
والذي يساوي تقريبا 1.83. ولكن ماذا يحدث اذا ما اضفنا ايضا بعض الكسور الاخرى بقيم اصغر فاصغر؟ لنجرب مع المثال التالي :
بالطبع الناتج سيكون اكبر من السابق, تقريبا 2.9. والجدول التالي يوضح ان الناتج يرتفع كلما ازدادت العناصر المضافة:
عدد العناصر المجموع (تقريبا) 1 1 10 2.9 100 5.2 1000 7.5 10000 9.8 100000 12.1 1000000 14.4 1000000000 21.3
والسؤال الذي يطرح نفسه: هل هناك حدّ يقف عنده ناتج الجمع كلما اضفنا عناصر اصغر الى المتسلسلات المتناسقة ( كالامثلة التي مرت )؟ ام ان نمو الناتج سيتمر دون توقف ؟
لكي نتمكن من الاجابة على هذا السؤال سنقسم الكسور الى مجموعات, وفي كل مجموعة سنضاعف عددها عن المجموعة السابقة. وليكن المثال التالي مع 8 عناصر ( لاحظ ان 8 تساوي 2 اس 3):
والتي تساوي:
ولا ننسى ان: النصف اكبر من الربع والذي بدوره اكبر من الثلث, واصغر العناصر المذكورة في المثال هو الثمن. وعليه يمكننا القول ان:
وبشكل عام فان:
فاذا كانت k=20 فان عدد العناصر يساوي 2 بقوة 20, اي 1048576 ( اكثر من مليون عنصر ), في حين ان ناتج جمع تلك العناصر بالكاد يتعدى الـ 11 مرتبة عما سبق (ارجع الى الجدول السابق)! بمعنى ان الناتج يرتفع ولكن ابطئ من حركة السلحفاة. بمعنى ان الناتج يتباعد عن سابقه الى ما لا نهاية كلما ارتفعت قيمة الـ k. هذا في حال كان مقام الكسر عددا بسيطا ( والمتسلسلة متناسقة ), ولكن ما هو الوضع في حال كان المقام عددا تربيعيا؟ لنرى المثال التالي:
وما زلنا نستخدم نفس الالية السابقة: نضيف عناصر اصغر فاصغر الى عملية الجمع, ولكن في هذا الحالة ( ان يكون التباعد ما بين العناصر تربيعيا) نصل الى مستوى معين, وهذا المستوى اقل من 2. وبشكل دراماتيكي يتوقف ناتج الجمع عند
وكما نلاحظ فان الاس في المتسلسلة التربيعية الاخيرة كان العدد 2, في حين ان الاس في المتسلسلة المتناسقة كان العدد 1. وهذا الامر بالغ الاهمية, لاننا يمكن ان نستنبط ما يلي:
- اذا كان الاس اكبر من واحد فان ناتج المتسلسلة سيتوقف عند مستوى معين.
- اذا كان الاس اصغر من واحد فان ناتج المتسلسلة سيتباعد الى ما لا نهاية.
وفي حال المتسلسلة المتناسقة حيث يكون الاس بقوة العدد 1 فان الناتج سيكون ما بين الحد وما بين التباعد اللا نهائي.
واذا كان السويسري الشهير ليونهارت اويلر (Leonhard Euler ) هو اول من استخدم دالة زيتا ( والتي تأخذ شكل الحرف الاغريقي ζ ) في القرن الثامن عشر, الا ان استخدامه لها كان محدودا حتى جاء الالماني برنارد ريمان (Bernhard Reimann) ليوسع نطاق البحث حتى برهن على كونها دالة جزئية الشكل ويمكن استخدامها ويمكن استخدامها حتى للاعداد المركبة, حتى وضع لها المتسلسلة التالية:
ويمكن استخدام قيم مختلفة لدالة زيتا. واكثرها شهرة هي (ζ(1 حيث تساوي اللا نهاية (∞), وذلك لان (ζ(1 متسلسلة متناسقة. واما فانها (ζ(2 تساوي تقريبا 1.6449 كما مر سابقا. وفي الواقع فانه اذا كانت قيمة s عددا زوجيا فان ناتج المتسلسلة لا بد وان يحتوي على ثابت الدائرة (العدد باي), واما اذا كان قيمة الـ s عددا فرديا فان الامر اكثر تعقيدا. فقد برهن اليوناني ابيري (Rger Apery) على ان (ζ(3 عددا غير نسبي. ولكن برهان ابيري لا يمكن ان نستخدمه مع (ζ(5 او (ζ(7 ...الخ.
فالمتغير s في دالة زيتا لريمان كما يمكن ان تكون بقيمة عدد حقيقي فانها يمكن ان تكون ايضا بقيمة عدد مركب ( حقيقي مع خيالي).
ومن خواصها ايضا ان هناك عدد لا متناهي من الجذور, بمعنى ان s يمكن ان تكون بعدد لا متناهي من القيم في حالة (ζ(s تساوي صفر.
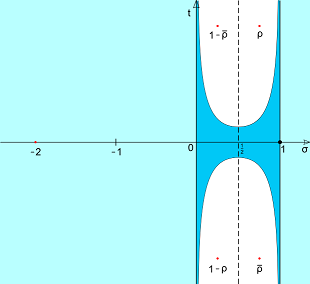
وفي احدى المقالات ادعى ريمان ان جميع جذور دالة زيتا تقع ضمن الخط العمودي حيث σ = 1/2 وانه لا جذور بعد σ = 1 او قبل σ = 0, في الشكل التالي:
اول محاولات اثبات دعوى ريمان كانت عام 1896 , فهناك من اثبت ان الجذور يجب ان تكون ضمن الاطار ما بين 0 و 1. وفي عام 1914 اثبت العالم البريطاني هاردي (Godfrey Harold Hardy) انه فعلا هناك عدد لا متناهي من الجذور عند الخط المستقيم 1/2 ولكن لا مانع من ان توجد جذور اخرى خارج هذا الاطار. وفي عام 1986 تم احصاء (1500000000) من تلك الجذور التي فعلا تقع عند الخط المذكور. وفي يومنا الحاضر تم التوصل الى اكثر من 100 مليار جذر.
وهذا الكم الهائل من الجذور يمكن ان يعطينا انطباع بصحة الحدسية, ولكن في نفس الوقت لا ينفي خطأها. فبحسب دعوى ريمان ان كل الجذور تقع عند الخط 1/2, وهذا ما يجب اثباته او نقضه.
ولكن ما اهمية حدسية ريمان؟
في الواقع هناك علاقة غير متوقعة ما بين دالة زيتا ريمان وما بين الاعداد الاولية التي لا تقبل القسمة الا على نفسها او على الواحد. ومن خلال الاعداد الاولية يمكن ان نوجد المتسلسلة التالية:
وهي متسلسلة جديدة للتعبير عن دالة زيتا ريمان, بمعنى ان المعلومات التي لدينا حول الدالة المذكورة يمكن ان تسلط الضوء على توزيع الاعداد الاولية وتعطينها فهما افضل لحجر الاساس في علم الرياضيات.
الرياضي الالماني ديفيد هليبرت (David Hilbert) والمشهور بالمعضلات الـ 23 في الرياضيات, ذكر في المعضلة الثامنة (لو سُمح لي بالرجوع الى الحياة بعد 500 عاما سيكون اول سؤال لي: هل تم اثبات فرضية ريمان؟). وللاسف الى اليوم لم يستطع اي شخص من اثبات او نفي فرضية ريمان!
وهاانتم قد حصلتم على كل المعلومات اللازمة حول الفرضية المذكورة, فاذا كنتم ترغبون بالحصول على مبلغ وقدره مليون دولار مقدم من معهد كلاي للرياضيات (Clay Mathematics Institute) ما عليكم الا تقديم برهان ـ دقيق ـ على صحة الفرضية او نفيها. ومن جهتي ساتمنى لكم كل التوفيق





 فرضية ريمان (Riemann hypothesis)
فرضية ريمان (Riemann hypothesis)
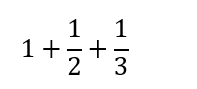
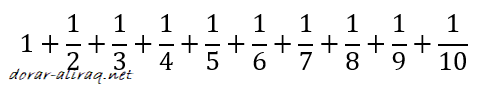
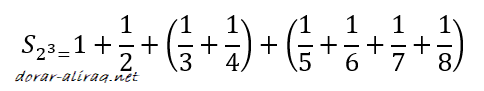
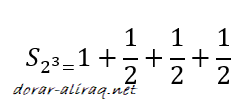
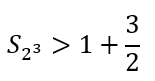
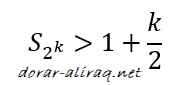
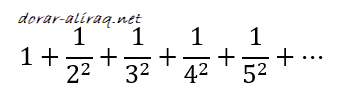
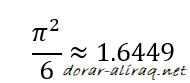
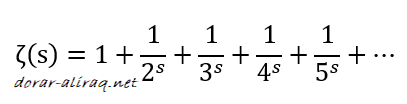
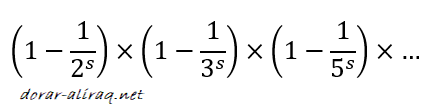

 رد مع اقتباس
رد مع اقتباس !
!  ~
~