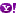الجبر هو البراعة في حل المسائل الحسابية والتفكير بالية صحيحة للحصول على الجواب. وتظهر براعة هذا العلم بطريقة التفكير بشكل عكسي. لتوضيح ذلك نضرب المثال التالي:
اذا ابتدأنا بالعدد 42 واضفنا اليه 15 فاننا نصل الى العدد 57. وطريقة التفكير هنا هي "مستقبلية", اننا اننا نبدأ بعدد ثم نضيف اليه او نحذف منه لنصل الى العدد النهائي.
ولكن ماذا لو عكسنا السؤال ليكون: ما العدد الذي اضفناه الى 42 ليصبح الناتج 57؟ بمعنى اننا ابتدأنا من النتيجة لنصل الى مقدمات المعادلة, فاسلوب التفكير هنا "عكسي".
ومثال اخر غالبا ما يستخدم مع الاطفال:
اذا كان هناك طفلا ما يبلغ مع العمر 6 سنوات في نفس الوقت الذي يبلغ والده عمر الـ 40 سنة, في ايّ عمر يجب ان يكون الوالد ليصبح اكبر من ولده بثلاث مرات؟
يمكن الجواب بمختلف الطرق والاساليب, ولكن الجبر اسهل وافضل طريقة:
وكخطوة اولى يجب ان نعثر على العلاقة ما بين عمر الطفل ووالده, ولا يتم ذلك الا من خلال ايجاد المعادلة المناسبة. واذا كان عمر الطفل اليوم هو (6+x) فان عمر والده (40+x).
ولان المطلوب هو ان يكون عمر الوالد ثلاثة اضعاف من عمر والده, يكون لدينا المعادلة التالية:
ومع بعض العمليات الحسابية نصل الى ان قيمة العدد المجهول (x) تساوي 11, بمعنى انه لكي يكون الاب اكبر من ولده بثلاث مرات يجب ان يبلغ سن الـ 51 في حين ان الولد سيكون بعمر الـ 17 عاما!!
وبنفس الطريقة اذا اردنا معرفة السن الذي سيتضاعف به عمر الوالد بالنسبة لولده ( نستبدل فقط العدد 3 بالعدد 2), لنصل الى 34 عاما للولد وضعفه (اي 68 عاما) للوالد.
وفي الواقع فان الامثلة سالفة الذكر هي من نوع المعادلة الخطية, وهي معادلات التي كل حد فيها هو عدد ثابت ولا تحتوي على اكثر من احتمال واحد وهو الاحتمال الصحيح. فالعدد المجهول فيها بقوة الرقم واحد.
اما لو كان العدد المجهول بقوة الرقم 2 او 3 فان المعادلة تصبح اما تربيعية او تكعيبية, وحينها ستتعدد احتمالات الجواب الصحيح وتكون المسألة اصعب من الخطية.
وفي الحقيقة فان الرياضيات خضعت للكثير من التغيير والتطور, فقد انتقلت من مجرد علم حسابي يستخدم الارقام فقط الى علم يستخدم الرموز والاشكال, والانتقال من الارقام الى الحروف هي خطوة عقلية تستحق الجهد والاهتمام.
ومن اهم انجازات العلمية في العصر الاسلامي هو علم الجبر الذي انشأه العالم المسلم ابو عبد الله محمد بن موسى الخوارزمي اثناء القرن التاسع ميلادي. وقد الف الخوارزمي كتابا بعنوان "كتاب المختصر في حساب الجبر والمقابلة" حيث وضع اسس علم الجبر والاساليب العملية لحل المعادلات الخطية والمعادلات التربيعية.
وبعد الخوارزمي بحوالي القرنين ظهر عالم مسلم اخر في بلاد فارس, غياث الدين عمر بن ابراهيم الخيام المعروف بعمر الخيام. وقد اشتهر عمر الخيام بشعره باللغة الفارسية المعروف باسم "الرباعيات". وفي عمر الـ 22 عاما الف كتابا تحدث فيه عن اسلوب حل المعادلات التكعيبية, ليكون بذلك اول من تناول هذا النوع من المعادلات. ولم تقتصر شهرة الخيام على هذا الامر فحسب, بل يعود اليه الفضل باستخدام الرمز (x) للدلالة على العدد المجهول, وذلك انه اول من استخدم مصطلح الـ (لا شئ) لينقل بعض ذلك الى البرتغالية ويختصر الى الـ (x).
واثناء عصر النهضة وتحديدا عام 1545 نشر العالم الايطالي جيرولامو كاردانو ( Girolamo Cardano) حل المعادلات من الدرجة الرابعة ( اي تلك التي يكون فيها العدد المجهول بقوة الرقم 4). وفي الواقع لا يعتبر كاردانو مبتكرا لهذا الاسلوب, لانه اعتمد بالاساس على طريقة حل المسائل التربيعية والتكعيبية التي وضعها الخوارزمي والخيام.
وبشكل عام فان الابحاث التي اجريت بهذا الخصوص اثبتت ان جميع المعادلات الجبرية سواء التربيعية او التكعيبية او حتى من المستوى الرابع يمكن حلها ـ وبشكل حصري ـ باستخدام الرموز والعمليات الحسابية التالية:
فمثلا المعادلة التالية:
فان النتيجة:
وبالطبع كلما ارتفع مستوى المعادلة اصبحت خطوات الحل اطول واصعب. وبسبب صعوبة حل المسائل التكعيبية ومسائل الدرجة الرابعة, ولانه في اغلب الاحيان نصل الى نتيجة تقريبية, فاننا لم نعثر على اي عالم قد وضع اسلوبا عاما لحل المسائل من الدرجة الخامسة ( تلك التي تحتوي على عدد مجهول بقوة الرقم 5).
ففي عام 1826 اعطى العالم النرويجي نيلز ابيل (Niels Henrik Abel ) , وهو في سن الـ 19, برهانا على انه يوجد اي حل جبري للمعادلات من المستوى الخامس. هذا البرهان لم يتقبله كل علماء الرياضيات بالرغم من عدم امكانية نقضه او اثبات عدم صحته. وحتى اليوم ما زال برهان ابيل ـ الذي كرم بعد وفاته وعدّ واحدا من عباقرة الرياضيات ـ قيد البحث.
على مدى خمسة قرون كان علم الجبر يعني "العلم النظري حول المعادلات", ولكل في القرن التاسع عشر اتخذ هذا العلم طريقا اخرا. حيث تحولت الرموز الجبرية من رموز تمثل الاعداد فقط الى علمات يمكن ان تمثل حتى الجمل والعبارات, وبالتالي صارت تستخدم حتى في المنطق. بل وابعد من ذلك, فقد اصبح للرموز الجبرية علاقة حتى بمتعددات الابعاد مثل المصفوفات, ويمكن ان تستخدم خارج نطاق الرياضيات حتى مع الـ "لا شئ".
ومن اهم الاحداث التي حصلت في تاريج "الجبر" الحديث هو ما جرى عام 1843 عندما ابتكر العالم الايرلندي وليام روان هاملتون ( Willial Rowan Hamilton) بما يعرف بالكواتيرنيون, وهو امتداد عملية غير تبديلية للاعداد المركبة ومجال تطبيقه في الدوران ثلاثي الابعاد وفي الرسوم الحاسوبية ثلاثية الابعاد.
في البدأ قام هاملتون نظام رموز يمكنه من خلاله توسيع الاعداد المركبة ثنائية الابعاد لتكون بعدد اكبر من الابعاد. ولعدة سنوات كان جهده منصبا على الوصول الى نظام ثلاثي الابعاد, لكن دون اي نتيجة او نجاح. واللطيف بالذكر ان هاملتون وفي كل صباح يتلقى سؤالا من ابنه "متى يمكن ان نستخدم الضرب مع الثلاثيات؟" وكان الجواب دوما: "لا يمكننا الا ان نستخدم الجمع او الطرح"!
وفي احد الايام واثناء نزهة مع زوجته خطرت ببال هاملتون فكرة كانت السبب وراء وصوله الى قمة النجاح, وملخصها ان يقوم باختبار الرموز رباعية الابعاد. دون هاملتون فكرته هذه على صخرة وجدها هناك وما زالت الى اليوم موجودة كتذكار عن هذه الحادثة قرب جسر (Brougham Bridge).
من خصوصيات الكواتيرنيون ان تبديل اماكن العناصر اثناء عملية الضرب امر بالغ الاهمية, بخلاف القوانين الموروثة عن الجبر الكلاسيكي والعمليات الحسابية المعتادة.
وفي الوقت الراهن فان اهمية الكواتيرنيون مع الجبر الخطي ( اسسه العالم الالماني هيرمان كراسمان) تبرز في الفيزياء والرسومات الحاسوبية وكذلك الاشكال الهندسية.
واثناء القرن العشرين كانت البديهية هي المهينة على علم الجبر, وقبل الجبر كانت البديهية هي الاساس التي بني عليها ما يعرف بالهندسة الاقليدية. ونعني بالبديهية تلك التي تكون نتائج مقدماتها صحيحة ولا تحتاج الى لبرهان او اثبات.
ولعل القرن العشرين كان ايضا مميزا بالنسبة الى الجبر, اذ في النصف الاول منه برز اسم العالمة الالمانية ايمي نوثير ( Emmy Noether) والتي اشتهرت بمساهمتها في ما يعرف بالجبر التجريدي او الجبر الحديث.
واحد اشكال الجبر التجريدي هو ما يعرف بتساوي الشكل, حيث انه اذا وجد تشابه شكلي ما بين بنيتين في الرياضيات فانه يقال انهما متساويتان شكلا.
والى اليوم ما زالت الجهود متواصلة للبحث في بحر علم الجبر..ولا ندري فقد يفاجئنا المستقبل لنجد اسما من الدرر ضمن مجموعة المبتكرين في هذا العلم.





 الجبر في الرياضيات
الجبر في الرياضيات
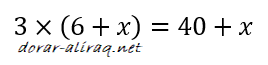
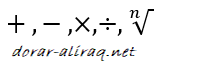
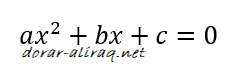
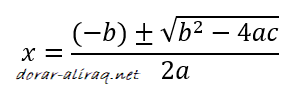
 رد مع اقتباس
رد مع اقتباس

 ويجوز انت
ويجوز انت