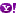تعد مبرهمنة فيرما الاخيرة واحدة من اشهر ما يعرف بالمعادلات الديفونتية, وهي المعادلات كثيرة الحدود والتي تحتوي على اكثر من متغير مجهول. واضافة الى اسلوب الحل المعقد اذ لا توجد صيغة معينة متفق عليها, فان المعادلات الديفونتية ( على اسم العالم اليوناني ديوفانتوس) لا تقبل باي جذر الا اذا كان عددا صحيحا.
وبالحديث عن العالم الفرنسي بيير دي فيرما (Pierre de Fermat) الذي عاش في القرن السابع عشر, وعمل في مجال القضاء كما كان مستشارا في برلمان تولوز المحلي, فانه كان ايضا عالم رياضيات يشار اليه بالبنان. وبالاضافة الى جهوده في نظريات الاحتمالات فقد اشتهر ايضا بمرهنته الاخيرة التي تنص على:
اذا كان كل من x,y,z,n اعداد صحيحة طبيعية , وكانت n اكبر من 2, فان
فنحن نعلم اننا لو جمعنا عددين تربيعين مع بعضهما البعض يمكن ان نحصل على عدد تربيعي اخر:
ولكن هل يمكن ان نحصل على عدد مكعب فيما لو جمعنا عددين مكعبين مع بعض؟ وما هو الصحيح فيما لو كانت الترقية (الاس) اكبر من ذلك؟
بحسب مبرهمنة فيرما فان ذلك من المستحيلات!
لم تنته الاثارة في المبرهنة المذكورة عند هذا الحد. فقد ادعى فيرما في هامش على نسخة من كتاب "الاحتمالات " لديفانتوس ـ حيث دون المبرهنة ـ انه عثر على برهان لدعواه تلك ولكن المجال لا يسع لتدوينه!! ليثير بذلك فضول علماء الرياضيات والهواة لاكثر من ثلاثة قرون.
اذا ما فكرنا بالمعادلة x+y=z فانه في الوهلة الاولى نشعر ببعض الصدمة, اذ كيف يمكن ان نعرف قيمة كل مجهول؟ ولا توجد اي احداثيات يمكن من خلالها معرفة الحل!
في الواقع هذا مجرد شعور خاطئ, فالمعادلة السالفة الذكر اسهل مما نتوقع. اذا انه يمكنك اختيار اي قيمة لاي متغير بشرط ان تصح المعادلة بحيث يتساوى شطرها الايمن مع الايسر.
فيمكن ان نختار 3 كقيمة للـ x و 7 كقيمة للـ y وبالتالي فان قيمة z تكون 10. ولا يوجد هناك من يمكنه الاعتراض على هذا الجواب.
وكذلك يمكن ان نبرهن على ان z لا تساوي 9 مع الابقاء على قيم المتغييرين الاخرين.
وبنفس الطريقة يمكن ان نحل المعادلات التربيعية من نوع
الفرق الوحيد هو ان كل متغير في المعادلات التربيعة مضروب مع نفسه. فاذا كانت x تساوي 3 فان تربيعها يساوي 9 , واذا كانت y تساوي 7 فان تربيعها يساوي 49. مما يعني ان تربيع z يساوي 58 وقيمة z هي الجذر التربيعي للـ 58. وقطعا يمككنا ان نقول اننا توصلنا الى الحل وايجاد القيم المطلوبة. ولكن علينا ان لا ننسى ما ذكرناه في بداية هذا الموضوع, ان المعادلات الديفونتية لا تقبل باي جذر ما لم يكن عددا صحيحا, والجذر التربيعي للعدد 58 للاسف ليس منها! وبالتالي فان القيم المقترحة لا تعتبر حلا للمعادلة المذكورة.
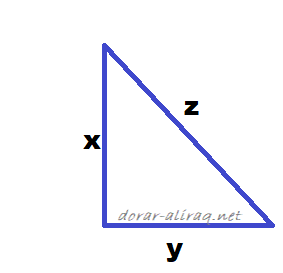
لنعيد النظر في المعادلة التربيعية المذكورة, اذ انها تذكرنا بنظرية فيثاغورس والعلاقة ما بين اضلاع المثلث قائم الزاوية:
حيث تقع الزاوية القائمة ما بين المتغيرين x و y. في حين ان z تعتبر طول الضلع المسمى بالوتر.
والجدير بالذكر ان كلا من x و y و z تسمى بثلاثية فيثاغورس.
وفي الواقع توجد الكثير من الاعداد التي تصلح ان تكون قيم لثلاثية فيثاغورس دون ان تخالف الشرط الاساسي للمعادلات الديفونتية. واصغر تلك القيم هي 3 و 4 للـ x و y و5 كقيمة للمتغير z.
وكذلك ما ذكرنا في بداية الموضوع 5 و 12 و بالتالي فان قيمة الـ z تساوي 13. او مثلا 20 و و21 لتصبح قيمة الـ z العدد 29.
هل يمكن تطبيق نفس المبدأ على المعادلات التكعيبية من نوع:
قد لا يبدو ذلك واردا. اذا اننا يمكن ان نعثر على قيم للمتغيرات في الاعداد التربيعية بكمية غير محدودة, في حين اننا لا نستطيع ان نجد ولا حتى قيمة واحدة بعدد صحيح طبيعي للمتغيرات في المعادلات التكعيبية. وذلك ما توصل اليه السويسري الشهير ليونهارت اويلر ( Leonhard Euler ) حيث ادعى: "انه لا يوجد اي جذر صحيح طبيعي للمعادلات الديفونتية اذا كان n اكبر من 2".
وكمحاولة للوصول الى حل يمكن ان نختار نبدأ باختيار قيم صغيرة للـ n. ففي حالة n =4 اسهل بكثير من n=3. والظاهر ان فيرما استخدم في برهانه القيمة 4 للمتغير n.
وفي القرنين الثامن عشر والتاسع عشر حاول العلماء مع مختلف القيم للمتغير n. فاويلر اختار القيمة 3 في حين ان الفرنسي ليجاندر ( Andrien Marie Legendre) حاول مع القيمة 5.
واما الفرنسي غابرييل لامي (Gabriel Lame) والذي توهم انه توصل الى البرهان فقد استخدم القيمة 7.
كما قامت الاكاديمية العلمية الفرنسية بمنح الالماني ارنشت كومر ( Ernst Kummer) جائزة نقدية بقيمة 3000 فرانك لكونه افضل من قدم برهان على حدسية فيرما, بالرغم من دركليه (Peter Gustav Lejeune Dirichlet) استطاع نقض برهان كومر.
وتقوم محاولة كومر على تجربة كل الاعداد الاولية دون الـ 100, باستثناء الاعداد 37 و 59 و 67, كقيم للمتغير n. ولكنه اخفق من اعطاء برهان عام يحل المعضلة, وكانت محاولته هي فعلا الافضل والتي ساهمت في جميع المحاولات اللاحقة.
وهكذا تلاحقت المحاولات ومنحت الجوائز وطرحت العديد من البراهين التي سرعان ما يثبت خطأها, حتى اعتبر العالم ان هذه الحدسية مما لا يمكن اثباتها او نفيها.
ولكن في عام 1995 عادت حدسية فيرما الى الاضواء مجددا, عندما قام عالم رياضيات بريطاني يدعى اندرو وايلز ( Andrew Weil), والذي شغلته هذه المعضلة وهو في العاشرة من عمره عندما قرأها في احد الكتب في المكتبة المحلية في كامبردج. وبعد سنين طويلة وتحديديا في عام 1993 اعلن وايلز ومن خلال محاضرات القاها في جامعة كامبردج عن برهانه, ولكن سرعان ما تبين خطأ ذلك البرهان.
ومع ذلك لم يستلم وايلز ولم ييأس من تحقيق حلم الطفولة, حتى اعاد النظر في برهانه ليصحح الاخطاء ويعلن عنه مرة اخرى عام 1995. وحتى يومنا الحالي لم يستطع اي احد من ايجاد ثغرة او خطأ في برهان اويلر.
لقب ويلز بـ "قاهر مبرهنة فيرما" وحصل على العديد من الجوائز اهمها, جائزة الملك فيصل العالمية عام 1998 واخرها جائزة ابل ( وهي تعادل جائزة نوبل) عام 2016.
والسؤال الان عن التاريخ الذي ينقض به برهان وايلز لتعود حدسية فيرما الى نقطة البداية!!





 مبرهنة فيرما الاخيرة
مبرهنة فيرما الاخيرة
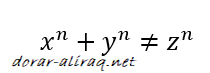
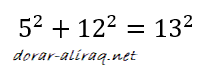
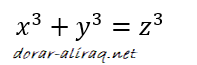
 رد مع اقتباس
رد مع اقتباس