العدد e او ما يعرف باللغة العربية بالعدد هـ او بالعدد النيبيري او عدد اويلر هو اخر الوافدين بالمقارنة مع منافسه الاوحد العدد باي او ما يعرف بثابت الدائرة. حيث ان ثابت الدائرة له تاريخ عريق تمتد جذوره الى عهد البابليين, في وقت لم يكن لعدد اويلر اي وجود يذكر. الا ان هذا الشاب المفعم بالحيوية سرعان ما سجل حضوره في كل يتعلق بـ "النمو", سواء كان الحديث عن النمو السكاني او الاقتصادي والمالي او اي كمية فيزيائية فانه لا غنى عن العدد e.
ولماذا كل هذه الاهمية للعدد e الذي تساوي قيمته تقريبا 2.71828؟
هذا العدد لم يأت بمحض الصدفة ليكون واحدا من اهم الاعداد الثابتة القيمة في الرياضيات. وكان اول ظهور له في بدايات القرن السابع عشر حيث كان علماء الرياضيات يبذلون الكثير من الجهد لتفسير وشرح فكرة اللوغاريتم; ذلك الاكتشاف الرائع الذي مكن ضرب الاعداد الضخمة الى ان تتحول الى عملية الجمع.
اثناء القرن السابع عشر تطور عدد اويلر كثيرا. ففي عام 1683 قام العالم السويسري الشهير ياكوب بيرنولي ( Jacob Bernoulli), احد افراد عائلة بيرنولي الشهيرة في عالم الرياضيات, بالعمل على مسألة ما تعرف "الارباح على الارباح":
فلو افترضنا انك ادخرت مبلغ 1 دولار (رأس المال) في البنك على ان تحصل على ارباح سنوية بنسبة 100%. وبالطبع لا توجد هكذا نسبة ارباح في عالم البنوك, لكن نفس الالية يمكن ان تجري على اي نسبة اخرى. وكذلك الحال فيما لو كان رأس المال اكثر من دولار.
و مع نسبة 100 % وبرأس مال يتكون من دولار واحد فانه في نهاية العام سيكون لديك دولاران. ولكن ماذا لو قسمنا نسبة الارباح على السنة؟ فلو افترضنا انك ستحصل على 50 % كل نصف سنة, فهذا يعني انه بعد النصف الاول من العام ستكون قد حصلت على 1.5 دولار, وفي نهاية العام سيرتفع المبلغ مع 0.75 دولار وستملك من خلال العام كاملا مبلغا وقدره 2.25 دولار.
وعن طريق اخذ الارباح على الارباح ستكون قد كسبت 0.25 دولار زيادة عما لو اخذت الارباح لمرة واحدة في السنة. بالطبع هذا المبلغ ليس بالكبير, لكن تخيل الفرق لو ان رأس المال مليون دولار او اكثر, اذ سيكون الفرق 25 الف دولار!
افترض الان ان نسبة الارباح تقسم على اربع مرات في السنة, في كل مرة تحصل على 25% من الارباح على اموالك الموجودة في البنك. وحينها سيكون رأس المال قد ارتفع الى 2.44141 دولار, اي بزيادة 0.44141 دولار عن الارباح لكل العام. واترك لك حساب ارباح المليون!
ذلك يعني انه كلما اخذنا نسبة ارباح اقل وفي فترات متقاربة سنكسب اكثر! هل يعني ذلك انك ستحصل على مبلغ قريب من المليون من خلال دولار واحد وخلال عام واحد؟
للاسف هذا الامر لا يمكن ان يحصل, لانه مجموع المبلغ يتجه نحو رقم ثابت كلما قلت الفترة الزمنية. وحتى لو اخذت ربحا على كل ثانية فلن تفرق عما لو اخذت لكل يوم. شاهد الجدول التالي ( مبني على اساس رأس مال من دولار واحد ونسبة ارباح 100 %.
الفترة الزمنية المبلغ النهائي بالدولار سنة كاملة 2.00 نصف سنة 2.25 ربع سنة 2.44141 شهر 2.61304 اسبوع 2.69260 يوم 2.71457 ساعة 2.71813 دقيقة 2.1828 ثانية 2.71828
وهذا الحد الذي وصلت اليه الارباح لو كانت لكل يوم هو ما اطلق عليه العلماء اسم e او هـ.
وقد تتساءل هل طريقة تقسيم الارباح بهذه الطريقة جيدة ام لا؟ الجواب: بالطبع ستكون جيدة فيما لو كانت الارباح لك, وستكون سيئة فيما لو اقترضت مبلغا ما من البنك.
وكما هو الحال مع ثابت الدائرة فان العدد e ايضا غير نسبي وبالتالي لا يمكننا تحديد قيمته على وجه الدقة. واذا ما اردنا فقط اول عشرين مرتبة عشرية فان العدد هـ يساوي:
2.71828182845904523536
وافضل تعبير واقربه الى قيمة عدد اويلر هو العدد الكسري 87/32, اذا كان كل من البسط والمقام لا يتكون الا من مرتبتين. اما اذا تكونا من ثلاث مراتب فان اقرب عدد كسري الى قيمة عدد اويلر هو 878/323. وهذا العدد التالي فقط تطور عن العدد الاول وباسلوب يمكن قرائته من اليمين او اليسار, او ما يعرف باسلوب ما لا يستحيل بالانعكاس.
واشهر متسلسلة للعدد e هي:
والتي يمكن كتابتها بطريقة اخرى:
وفيما يبدو فان العدد e يتبع نمطا معينا وهو اكثر قياسية من ثابت الدائرة. واما كونه عددا غير نسبي فقد تم اثباته على يد العالم العالم السويسري الشهير ليونهارت اويلر ( Leonhard Euler) والذي سمي هذا العدد باسمه.
وفي عام 1840 اثبت عالم الرياضيات الفرنسي جوزيف ليوفيل ( Joseph Liouville ) ان عدد اويلر لا يمكن ان يكون جذرا لاي معادلة تربيعية. وعالم فرنسي اخر, وهو الشهير تشارلز هيرمت ( Charles Hermite ) اثبت في عام 1873 ان عدد اويلر لا يمكن ان يكون جذرا لاي معادلة جبرية.
والجدير بالذكر انه بعد 9 سنوات استخدم الالماني فريدينوند فون ليندمان ( Ferdinand Von Lindemann) نفس اسلوب هيرمت ليبرهن على ان ثابت الدائرة عددا متسام, اي انه لا يمكن ان يكون حلا لاي معادلة حدودية.
علاوة على اشتراكهما بكونهما اعدادا متسامية فان هناك نقطة تشابه اخرى ما بين عدد اويلر وثابت الدائرة, حيث ان قيمة عدد اويلر كاساس وثابت الدائرة الاس قريبة جدا من قيمة ثابت الدائرة كاساس مع عدد اويلر يمثل الاس. مع انه باستراق النظر الى الالة الحاسبة يمكن ان ندرك ان العدد الاول اكبر بقليل من العدد الثاني.
وللذكر فان العدد حيث يكون عدد اويلر اساس وثابت الدائرة اس يسمى بثابت غيلفوند, نسبة الى الروسي الكسندر غيلفوند ( Aleksandr Gelfond), ومن خصائصه انه ايضا عدد متسام.
ولكن يختلف الحال مع العدد حيث يكون ثابت الدائرة الاساس وعدد اويلر الاس, فلا نملك الكثير من المعلومات ولم يبرهن احدا فيما اذا عددا غير نسبي او متسام.
وكما ذكرنا في مقدمة هذا الموضوع فان اهمية عدد اويلر تكمن في حساب عمليات النمو, مثل النمو الاقتصادي و النمو السكاني.
كذلك يمكن ان نرى اثار لعدد اويلر في عمليات حسابية لا تتعلق بالنمو. فمثلا في القرن الثامن عشر قام الفرنسي بيريه مونتمورت ( Pierre montmort) بالبحث في نظرية الاحتمالات. فلو افترضنا ان مجموعة من الاشخاص ارادوا الخروج من مكان ما واخذ كل واحد منهم قبعة على امل ان تكون له. فما هي نسبة الاحتمال لكل شخص انه اخذ القبعة التابعة له؟ ان احتمال ان يكون كل شخص قد حصل على القبعة الصحيحة هو نتيجة تقسيم العدد واحد على عدد اويلر والذي يساوي تقريبا 37 %. واحتمال ان يكون هناك على الاقل شخص واحد قد حصل على قبعته هو بنسبة 63 %.
واكثر المعادلات روعة في عالم الرياضيات هي تلك التي تحتوي على عدد اويلر. فاذا ما تحدثنا عن اكثر الاعداد شهرة فاننا لا نتجاوز الاعداد ( صفر, واحد, ثابت الدائرة, عدد اويلر, والعدد التخيلي i الذي يساوي الجذر التربيعي لسالب واحد). وتجتمع كلها في:
وهو ما يعرف بمتطابقة اويلر!!!!
ولعل المعاني الحقيقة للـ e بقيت غامضة وحبيسة علم الرياضيات. والا فلماذا يوجد روائي ومؤلف بحجم ارنست فينسنت رايت (Ernest Vincent Wright) يكتب رواية بعنوان (Gadsby ) من 5000 كلمة لا تحتوي اي منها على الحرف e؟؟!! لا يمكنني ان اتخيل ان هناك عالم رياضيات قادر على تأليف كتاب رياضيات دون ان يستخدم الحرف e!
ختاما, اهدي اليكم المواضيع التالية والتي لها علاقة بما ذكر في هذا الموضوع:
-رواية GADSBY - تأليف Ernest Vincent Wright
- ثابت الدائرة باي





 عدد أويلر المعروف بالرمز e
عدد أويلر المعروف بالرمز e
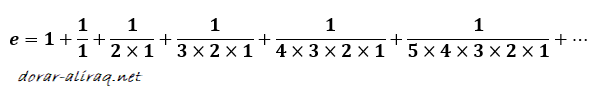
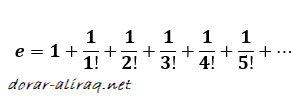
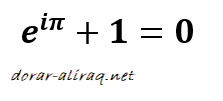
 رد مع اقتباس
رد مع اقتباس
 وماعندي هاي المعلومات عنه
وماعندي هاي المعلومات عنه 
