بسم الله الرحمن الرحيم
بين الحين والاخر, ولهيمنة الحساب على مختلف مجالات حياتنا, نكون مضطرين الى العودة الى مبادئ واسس الرياضيات. بمعنى اننا نعود الى اساسيات الحساب مثل الـ 1,2,3,4,5....الخ.
ان التعبير 4=2*2 يعني اننا يمكن ان نقسم الاعداد الى مكوناتها الاساسية. وبالطبع فاننا نستطيع ان نقسم اعدادا اخرى, مثل 6=3*2 , 8=2*2*2, 9=3*3, 10=5*2
فان كلا من ( 4 و 6 و 8 و10 ) كلها اعداد مركبة لانها تتكون من اعداد جدا اولية (2 و 3 و 5). فالاعداد الغير قابلة للتقسيم مثل (2 و 3 و 5 و 7 و 11 و 13...الخ) تسمى اعدادا اولية. حيث ان الاعداد الاولية هي تلك الاعداد التي لا تقبل القسمة الا على نفسها او على الواحد.
بناءا على هذا التعريف, وبالرغم من ان علماء الرياضيات في السابق كانوا يتعاملون مع الواحد على انه عدد اولي, فان علماء اليوم يعتبرون ان العدد 2 هو بداية الاعداد الاولية.
ان دراسة الاعداد الاولية يعيدنا الى ابسط الاساسيات في علم الرياضيات. فاهمية الاعداد الاولية لعالم الرياضيات هي بالضبط كاهمية الذرة في علم الكيمياء. فكما في الكيمياء تتكون جميع المركبات والتفاعلات من ترابط الذرات فيما بينها فان الاعداد في الرياضيات تتركب من الاعداد الاولية.
ونتيجة لذلك وضع العلماء نظرية تحمل الاسم "نظرية تحليل الاعداد الاولية" والتي تنص على: ان كل عدد صحيح وطبيعي اكبر من 1 يمكن التعبير عنه بطريقة واحدة من خلال ضرب الاعداد الاولية مع بعضها البعض. حيث ان العدد 12= 2*2*3 ولا توجد اي طريقة اخرى لتحليل العدد 12 الى اعداده الاولية. وحتى نظام الاس والاساس فان العدد 12 يكتب باسلوب (3*2^2).
مثال اخر: العدد (6545448) يحلل الى :
للاسف لا توجد اي معادلة او قانون يمكن استخدامه للوصول الى الاعداد الاولية. كما لا تتوفر معلومات كافية يمكن من خلالها ان نعرف كيف دخلت الاعداد الاولية ضمن الاعداد الصحيحة. واول الاثار لمحاولات الوصول الى الاعداد الاولية تعود بنا الى العالم الاغريقي اراتوستينس, والذي اشتهر بحساباته الدقيقة لمحيط الارض والتي كانت وما زالت محط اعجاب واندهاش.
فقد دوّن اراتوستينس الاعداد امامه ثم وضع خط تحت العدد 2 وقام بشطب كل مضاعفاته, وهكذا فعل مع العدد 3. ولان العدد 4 تم شطبه لانه من مضاعات العدد 2 فانه تجاوز الى العدد 5. وهكذا مع سائر الاعداد المدونة حتى لم يبق امامه الا بعض الاعداد, والتي كانت اعدادا اولية.
لذلك فاننا يمكننا التنبؤ بالاعداد الاولية. لكن كيف يمكن ان نحدد ما اذا كان عددا ما اوليا ام مركبا؟ ماذا يمكن ان نعتبر مثلا العدد (19071) او العدد (19073)؟
بغض النظر عن العدد 2 والعدد 5 فان العدد الاولي يجب ان ينتهي بـ 1 او 3 او 7 او 9. لكن ذلك لوحده لا يكفي لان نجزم بان عددا ما اوليا فقط لانه ينتهي باحد تلك الارقام ما لم نختبر احتمالات العوامل الاخرى. فالعدد (19071) يساوي:
فالعدد 19071 عدد مركب وليس اولي, بخلاف العدد 19073.
وهناك تحد اخر, وهو توزيع الاعداد الاولية. فمثلا لنرى كم عددا اوليا في كل 100 عدد ضمن المجال من واحد الى الف؟
المجال كمية الاعداد الاولية 1-100 25 101-200 21 201-300 16 301-400 16 401-500 17 501-600 14 601-700 16 701-800 14 801-900 15 901-1000 14 1-1000 168
في عام 1792, وعندما كان في سن الخامسة عشر, اقترح عالم الرياضيات الالماني الشهير كارل فريدريش غاوس اعطاء دالة تقريبية P(n) للاعداد الاولية الاصغر من n. فاذا كانت n تساوي 1000 مثلا فانه بناءا على معادلة غاوس يكون لدينا 172 عددا اوليا. ولكن الصحيح ان الاعداد الاولية ضمن المجال 1000 تساوي 168 عددا, اي اقل من تقدير غاوس. وهذا الحال ينطبق مع كل عدد n.
ولكن للاعداد الاولية دائما مفاجئات. ففي حالة ان n=10^371 ( عدد عملاق يتكون من العدد 1 يتبعه 371 صفرا) يتجاوز العدد الفعلي لتقدير كمية الاعداد الاولية. وهذا هو الواقع, فان تقدير الاعداد الاولية يختلف عن العدد الفعلي بزائد او ناقص.
في الواقع ان هناك عدد لا متناهي من الاعداد الاولية. وقد ذكر عالم الرياضيات اليوناني اقليدس في كتابه "العناصر" ( الكتاب 9, التعريف 20): "ان كمية الاعداد الاولية اكبر من اي عدد معين من تلك الاعداد". ولاثبات ذلك ساق اقليدس البرهان التالي:
لنفترض ان P هو اكبر عدد اولي, وان N=(2*3*5*...*p). فاذا كان N عددا اوليا نكون قد توصلنا الى عدد اولي اخر اكبر من P , وهذا مخالف للفرض.
واذا لم يكن N اوليا فانه يجب ان يكون قابلا للقسمة على عدد اولي, q. وهذا يعني ببساطة ان q ايضا مقسم للعدد (N-2*3*5*...*P) والذي يساوي 1, بمعني ان q يمكن ان يقسم ايضا الـ 1. وهذا تناقض لان كل الاعداد الاولية اكبر من الـ 1.
اذاً بغض النظر عما اذا كان N عددا اوليا ام مركبا فاننا نقع في دائرة التناقض, وبالتالي فان فرض ان P هو اكبر الاعداد الاولية لا يمكن ان يكون صحيحا.
وكون كمية الاعداد الاولية غير متناهية لم تقف كحجر عثرة امام طموح الانسان وفضوله بالوصول الى اكبر عدد اولي.
واكبر ما توصل اليه الانسان هو عدد ميرسن الاولي, المنسوب الى الراهب الفرنسي مارين ميرسن, والذي يساوي
(تم اكتشافه اواخر العام الماضي)
ومن اكثر المعضلات غير المحلولة في موضوع الاعداد الاولية هي ما تسمى بحدسية غولدباخ والمنسوبة الى عالم الرياضيات الالماني كريستيان غولدباخ. وتنص هذه الحدسية على: ان كل عدد صحيح وطبيعي وزوجي اكبر من 2 يمكن كتابته على شكل مجموع عددين اولين" وتسمى هذه الحدسية ايضا باسم "توائم الاعداد الاولية", بحيث ان هذا التوائم تكون متلاحقة ولا يفصلها الا عدد زوجي مثل العدد 12 وتأوميه الـ 11 والـ 13.
ومع اننا لا يمكننا البرهان على ذلك فان توائم الاعداد الاولية ايضا غير متناهية. مع انه ما زال لدى العلماء امل في الحصول على برهان يثبت صحة هذه الحدسية. فقد استطاع العالم الصيني شان جينكوغ من اثبات ان كل عدد زوجي هو ناتج جمع عدد اولي مع عدد نصف اولي ( وهو عدد ناتج من عملية ضرب عددين اوليين مع بعضها البعض). كما ان الفرنسي بيير دي فيرما اثبت ان العدد الاولي ضمن الصيغة (4K+1) يمكن كتابته بالاعداد التربيعية. مثل:
ولكن في الصيغة التالية (4K+3) لا يمكن التعبير عن الاعداد الاولية بنفس الاسلوب, فان العدد 19 لا يساوي:
واذا ما زلتم تذكرون فاننا وصفنا الاعداد الاولية بانها النواة والذرة لعلم الرياضيات. وقد يعترض معترض فيقول: ان الفيزياء تدخلت كثيرا في الذرة والنواة واستطاعت الكشف عن الكثير من خواصها وسياقة الاف المعادلات على اساسها. بينما الرياضيات وقفت في مكانها لا تبارحه اتجاه الاعداد الاولية.
وللجواب فاننا نأخذ العدد 5 وهو عدد اولي لابد وان يبقى على شكله دوما وابدا. ولكن يمكن التعبير عنه ايضا بالاسلوب التالي:
حيث ان: i هو الجزء التخيلي في نظام الاعداد, والذي يساوي:
فعلي هذا الاساس فان العدد 5 ليس عددا غير قابل للقسمة كما ذكرنا في بداية هذا الموضوع.





 الاعداد الاولية
الاعداد الاولية
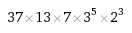
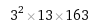
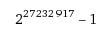
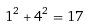
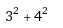
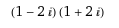
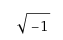
 رد مع اقتباس
رد مع اقتباس