إقليدس السكندري (Euclid of Alexandria) رياضي إغريقي عاش منذ أكثر من 2000 عام مضت، وكثيرًا ما يُطلق عليه لقب أبو الهندسة. يعد كتابه “الأصول” – “The Elements” أحد أكثر الكتب نجاحًا في التاريخ، ويقول البعض أن الكتاب المقدس هو الكتاب الوحيد الذي نُشر أكثر منه. يُعد ذلك الكتاب أيضًا أول طرح نظامي عن الهندسة. وضع فيه إقليدس قواعد الهندسة.
كان إقليدس مهتمًا بجميع الأشياء التي يمكن فعلها باستخدام حافة مستقيمة (مسطرة بدون ترقيم) وبوصلة.
ووضع مجموعته الخاصة من خمس قوانين تصف بعض الأشياء البسيطة التي يمكن فعلها بتلك الأدوات، بالإضافة إلى بعض الحقائق حول الزوايا والخطوط التي رأى أنها صحيحة بشكل بديهي ولا حاجة لتوضيحها.
المسلمات postulates : هى اشياء نسلم بصحتها بالسليقة بدون اقامة البرهان على صحتها. وهي :
- يمكن رسم خط مستقيم يصل أي نقطتين في الفراغ، وتسمى بالقطعة المستقيمة.
- يمكن إيجاد قطعة مستقيمة ذات أي طول. (أي أنها قد تمتد إلى ما لانهاية).
- بمعلومية نقطة وقطعة مستقيمة تبدأ من تلك النقطة، يمكن رسم دائرة متمركزة حول تلك النقطة ويساوي نصف قطرها طول القطعة المستقيمة.
المسلمات الثلاث الأولى
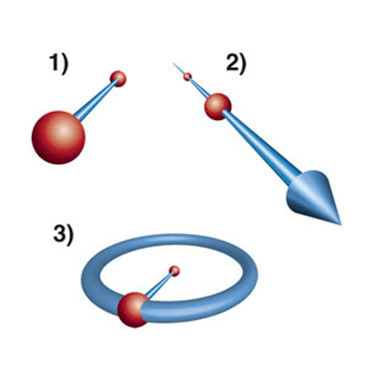
4- كل الزوايا القائمة متساوية.
(قد يبدو غريبًا لك الحاجة إلى توضيح ذلك، إذ أن كل الزوايا القائمة قياسها 90 درجة، وبالتالي فهي بالتأكيد متساوية. لكن ذلك لم يكن تعريف إقليدس للزاوية القائمة، إذ لم يكن لديه وسيلة لقياس الزاوية بالدرجات (الزاوية القائمة عند إقليدس هي أي زاوية تنتُج عن تقاطع مستقيمين بحيث يتساوى قياس الزاويتين الناتجتين عن التقاطع).
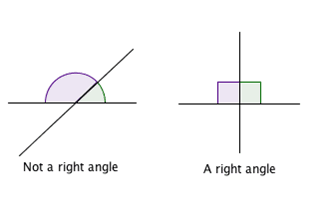
5- عند رسم قطعة مستقيمة بحيث تتقاطع مع مستقيمين، ويكون مجموع قياس الزاويتين الداخليتين الناتجتين من التقاطع أقل من مجموع زاويتين قائمتين، فإن المستقيمين يتقاطعان.ثمة العديد مما يمكن فعله باستخدام مسلمات إقليدس، كرسم شكل سداسي منتظم.
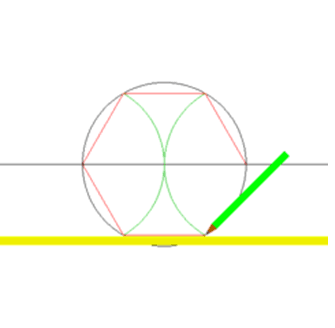
أو يمكنك تنصيف زاوية. أي قسمها إلى زاويتين متساويتين.
بالفعل تلك هي الأدوات والطرق التي استخدمها العمال لصنع الزينات والنوافذ الجميلة في الكنائس والأديرة.
لكن المسلمة الخامسة سببت بعض المشاكل للرياضيين؛ فقد ظنوا أنها يجب أن تتبع كاستنتاج من المسلمات الأربع الأولى. وقد قادت محاولتهم لبرهنة ذلك في النهاية إلى اكتشاف عالم الهندسة اللاإقليدية الغريب والعجيب.
اما البديهيات axioms:
فهى اشياء صحيحة بالبديهة و نقوم بالتسليم بصحتها كما هي بدون نقاش.والفارق بين المسلمات و البديهيات ان الشكوك اللتى قد تحوم حول المسلمات مبررة أكثر من اللتى قد تقوم حول البديهيات. بمعنى ان التشكيك في البديهيات أصعب من التشكيك في المسلمات.
البديهيات الخمسة axioms هى:
- 1 الأشياء المساوية لغيرها متساوية فيما بينها
- 2 اذا اضفنا كميات متساوية إلى اخرى متساوية تكون النتيجة متساوية
- 3 اذا طرحنا كميات متساوية من اخرى متساوية تكون النتيجة متساوية
- 4 الأشياء المتطابقة متساوية
- 5 الكل أكبر من الجزء
تعريفات اقليدس definitions نسردها فيما يلي:
- 1 النقطة هى مالا جزء له.
- 2 الخط هو طول بلا عرض
- 3 نهايتا الخط هما نقطتان
- 4 المستقيم هو خط يتطابق مع استواء النقاط اللتى تقع فوقه
- 5 السطح هو ماله طول وعرض فقط
- 6 حواف السطح هى دائما خطوط
- 7 المستوى هو سطح يتطابق مع استواء الخطوط المستقيمة اللتى تقع فوقه
- 8 الزاوية المستوية هى الميل بين خطين يلتقيان في مستوى ولا يواصلان امتدادهما
- 9 اذا كان خطا الزاوية مستقيمين سميت الزاوية مستقيمة الخطوط rectilinear
- 10 اذا قابل مستقيم اخر وبحيث صنع زاويتين متجاورتين متساويتين سميت الزاويتان قائمتين. و سمى المستقيم عمودي على الأخر
- 11 الزاوية المنفرجة أكبر من القائمة
- 12 الزاوية الحادة اصغر من القائمة
- 13 الحد هو ذلك حيث ينتهى شئ
- 14 الشكل هو ذلك المحصور بين حدوده
- 15 الدائرة هي شكل مستوى. حدها خط. وبحيث تكون المسافة بين نقطة ما داخل الدائرة وأى نقطة على الحد متساوية
- 16 مركز الدائرة هو النقطة في منتصف الدائرة السابق ذكرها
- 17 قطر الدائرة هو قطعة مستقيمة تمر بمركز الدائرة وينهى طرفاها على محيط الدائرة ويقسم القطر الدائرة إلى نصفين متساويين
- 18 نصف الدائرة هى الشكل المحصور بين قطر الدائرة و قوس الدائرة المقطوع بواسطة هذا القطر
- 19 متعدد الأضلاع هو الشكل اللذى حدوده خطوط مستقيمة فثلاثى الأضلاع يتكون من 3 اضلاع و رباعى الأضلاع يتكون من 4 اضلاع ومتعدد الاضلاع يتكون من عدد غير معين من الأضلاع
- 20 بالنسبة لثلاثى الاضلاع يسمى مثلث متساوى الاضلاع اذا كان طول كل اضلاعه متساوي ويسمى متساوى الساقين اذا كان ضلعان منه فقط متساويان ويسمى غير متساوى الاضلاع اذا كانت كل اضلاعه مختلفة في الطول
- 21 بالنسبة لثلاثى الاضلاع يسمى مثلث قائم اذا كانت احدى زاوياه قائمة ويسمى مثلث منفرج اذا كانت احدى زاوياه منفرجة ويسمى مثلث حاد اذا كانت كل زاوياه حادة.
- 22 بالنسبة لرباعى الاضلاع يسمى مربع اذا كانت كانت كل اضلاعه متساوية وكل زواياه قائمة ويسمى مستطيل اذا كانت كل زاوياه قائمة ولكن ليست كل اضلاعه متساوية ويسمى معين اذا كانت كل اضلاعه متساوية ولكن زواياه ليست قائمة ويسمى متوازي اضلاع اذا كان كل ضلعان متقابلان متساويين وكانت كل زاويتان متقابلتان متساويتين. اما باقى الاشكال الأخرى تسمى منحرفة.
- 23 المتوازيان هما مستقيمان يقعان في نفس المستوى ومهما مدناهما من كلا طرفيهام فهما لا يلتقيان.






 رد مع اقتباس
رد مع اقتباس