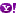توبولوجيا (Topology) هي كلمة يونانية من شقين (Topos-logos) أي علم المكان، علم يدرس الأشكال الهندسية بطريقة مختلفة عن علم الهندسة.
فالتوبولوجيا تتجاهل الأحجام والمساحات والزوايا والتي تمثل القضايا الأساسية في دراستنا للهندسة! في الهندسة ندرس المستطيل والمربع وغيره من الأشكال، واضعين قوانيناً للمساحة والحجم وقياسات الزوايا و و و..
أما في التبولوجيا فنحن نتجاهل كلَّ هذه الأمور، حيث لا تهمنا المساحات وقياسات الزوايا، فالمربع والمستطيل هما نفس الشّيء تبولوجيّاً، كذلك متوازي الأضلاع وشبه المنحرف، كل الأشكال الرباعية هي ذاتها تبولوجيّاً. وإذا نظرنا أبعد من ذلك، بتجاهلنا للزوايا يصبح أيضاً المثلث كالمربع والمخمّس والشكل السداسي، كل هذه الأشكال تمثّل شكلاً واحداً في التبولوجيا.
إذاً هل تقول التبولوجيا أنه لا فرق نهائياً بين الأشكال الهندسية؟ بالطبع لا، ولكن الأمور التي نأخذها بعين الاعتبار في التبولوجيا مختلفة عن الهندسة، التبولوجيا تهتم بطبيعة تمدد الشكل واستمراريته، أي تعتبر أن الشّكل لا يزال هو ذاته مهما تعرض للمط دون تمزيق. لنبسط الأمر أكثر: لنتخيّل كل شكل من الأشكال مع نملة صغيرة، ونراقب سير النملة على هذا الشّكل، سنلاحظ أن النملة ستسير على مربع بشكل مستمر ومتصل ولن تتجاوز خلال سيرها عليه أيّة حافة، لذلك سيكون المربع كالمستطيل كأي شكل ممتد دون وجود حفر ووجوه أخرى حيث تضطر النملة لكسر هذه الاستمرارية في سيرها.
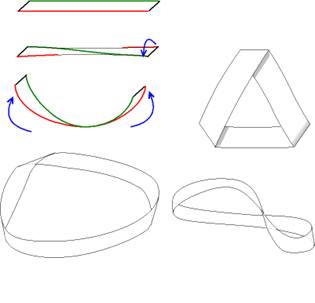
لدينا مثلاً شريط موبيوس الشهير:
هندسياً شريط موبيوس يستحيل أن يطابق المربع، ولكن طبولوجياً هما ذات الشكل، كيف ذلك! كي تمسح النملة كل أجزاء الشريط ستمشي عليه بسلاسة دون تجاوز أي حافة، و كأنها تمسح بسيرها مربعاً، بينما لو لم يتم وصل طرفي الشريط بهذه الطريقة فالنملة لن تمسح بسيرها المستمر إلّا وجهاً واحداً من الشريط، وكي تمسح وجهه الآخر ستضطر أن تتجاوز الحافة بين الوجهين. لذلك الشريط العادي وشريط موبيوس مختلفان تبولوجيّاً.
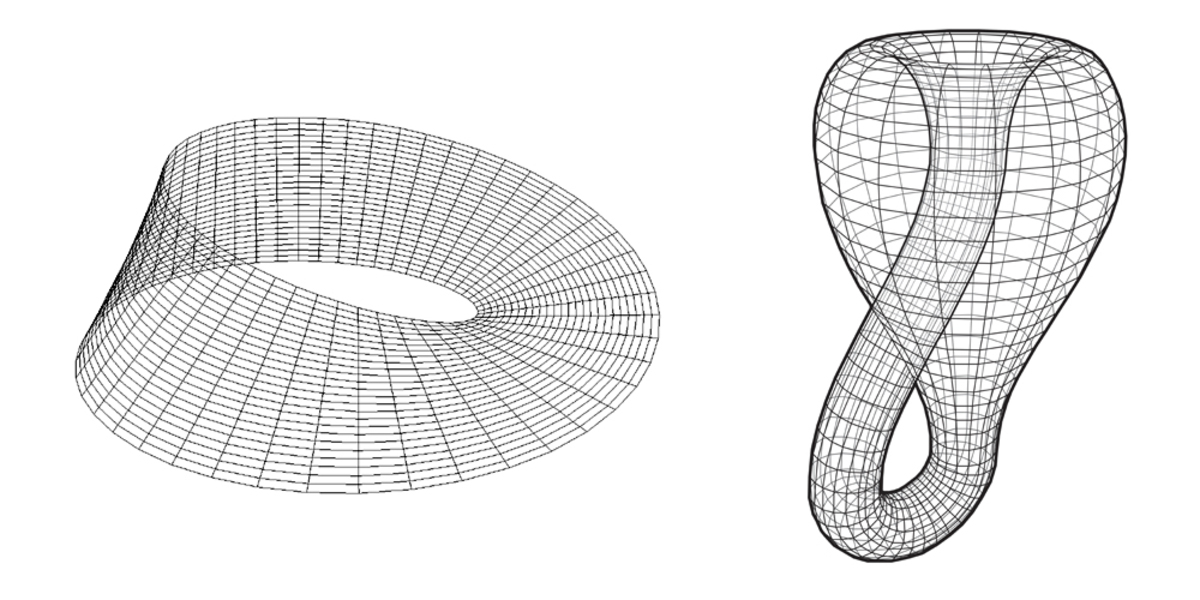
كذلك الطبولوجيا تهتم للحُفر في المجسمات، فمثلاً لدينا كرة، مهما ضغطناها وغيرنا من استطالتها فستبقى ذات الشكل تبولوجيّاً، فُكًرة البيسبول هي ذاتها كرة القدم هي ذاتها كرة التنس، أما لو تخيلنا أنها مفرغة على شكل أنبوب فسيختلف الأمر، ستصبح في عالم التبولوجيا كقطعة الدونات أو الإطار.
أشكال كهذه تسمى بالـ (منطويات - (manifolds، حيث يطلق هذا المصطلح على كل شيء يبدو كسطح ولكنه يصبح في أبعاد أعلى شكلاً أخر، فمثلاً اعتقد القدماء أن الارض مسطحة لأنهم يرصدونها ضمن مستوى قريب، ولكن في الأبعاد الأعلى هي ليست مسطحة.
هنا نميز بُعدين: بعداً ذاتياً وبعداً خارجياً، والبعد الذي غالباً ما نتحدث عنه هو البعد الذاتي. وهذا يعني أنَّ المنحني هو منطوي أحادي البعد، والسطح هو منطوي ثنائي البعد. ولكن هل يمكن تصنيف المنطويات طبقاً للأبعاد وتقديم طريقة للتحقق منها ومعرفة إلى أي صنف ممكن وضعها؟ إنَّ هذه المسألة باختصار غير محلولة حتى الآن! يمكن القول أنها مفهومة بشكل كامل في الأبعاد الصفرية والواحدية والثنائيّة، وأيضاً بشكل جيّد في خمسة أبعاد وأعلى. ولكنها تبدو غامضة جداً في ثلاثة وأربعة أبعاد.
إذا كان هذا يبدو غريباً، فلتتذكر أنَّ الأبعاد الذاتية الصّفرية والواحدية والثنائية تقابل في البعد الخارجي الأبعاد الثلاثيّّة التي يمكن تخيّلها والتي نعيش أصلاً فيها بسهولة. ولكن تصور العيش في البعد الرابع الإقليدي على الأقل! نحتاج هنا إلى إثبات رياضي أكثر من رسم صورة والتحديق بها.
ولكن عندما نصبح في البعد الخامس نصبح فجأة قادرين على استيعاب الوضع مرة أخرى. ألا يوجد تناقض؟! يعود سبب استيعاب هذه الأبعاد إلى خدعة ويتني "Whitney Trick" التي تسمح بنقل الأجسام المعقدة وفصلها إلى أجزاء مفهومة في البعد الخامس وما فوق. هذا يعني أنَّنا تركنا البعد الثالث والرابع.
عمليّاً هذه الفجوة في عدم استيعاب أجزاء من الموضوع لا يساعد على جعله أكثر تطبيقياً، ولكنه يسمح للنظريات والدراسات التي يعمل الفيزيائون عليها لسنوات عديدة بالتّقدم. ففي عام 1980م درس العالم سيمون دونالدسون جسيمات تسمى "instantons" التي لها علاقة بنظرية الجسيمات دون الذرية والقوى بينها بمنطويات رباعية الأبعاد، حيث أنّنا نعيش في منطوي رباعي البعد إذا أخذنا عامل الزمن. وقد أحدثت هذه الدّراسة ثورة في فهمنا للمنطويات رباعية الأبعاد.
في هذه المرحلة ما أهميّة هذا في عالمنا؟ إن أهم دور يلعبه أيُّ بحث هو الفهم النّقي للمسألة، كجزء من الرياضيات النظرية ينبغي علينا أن نسعى لفهم كلّ شيء غامض، وكلما زاد فهمنا للموضوع أكثر سنكون قادرين على تعامل مع التحديات التي تواجهنا في المستقبل. فإذا كنا نركز فقط على المشاكل التي لها تطبيقات مباشرة، فنحن في خطر أن نكون غير قادرين على معالجة المشاكل المستقبلية، وقد ينتهي الأمر إلى حل المشاكل بطريقة خاطئة. وقد أظهر مسار التاريخ البشري أن العديد من القفزات الكبيرة في المجالات العلميّة تأتي من مصادر غير متوقعة، والبحوث الأساسية غالباً ما تعطي ثمارها ربما بعد مئة سنة.
لذلك علماء الرياضيات حالياً يسعون لحل هذا "التّناقض" في التبولوجيا وإعطاء مفهوم أكثر تجريداً للمسألة، لتعميق فهمنا لكل شيء يمكننا أن نتصوره، وقد يكون هذا المفهوم نقطة البداية في استيعاب مفاهيم جديدة وعلوم أخرى.





 رد مع اقتباس
رد مع اقتباس