مجموعه من الاصدقاء واكفين سوى
فواحد من الاصدقاء انتقد شخص فقال عليه خل يولي هذا كلشي ما يفهم الغبي حتى 13 في 11 ما يعرف جكد


فجانت هاي ردة فعل الواقفين لان محد يعرف مضروب الرقمين جكد بالقليل قبل ان تجرب بالحاسبه او بطريقة الحساب التقليديه
طيب واذا عرفت اكو طريقه نكدر نعرف بيه الارقام الي متكونه من رقمين المضروبه بال 11 بصوره سريعه
معقوله
اي اي
مثلا
11*12 = 132
11*23 =253
11*34=374
اذا لاحظنه بالامثله السابقه ان اول رقم واخر رقم يتكررن نفسهن والي بالمنتصف حاصل جمع الرقمين
يعني 12*11 = اول ما نجمع 1+2 = 3 هذا نضعه بالمنتصف ما بين 1و 2 فيصر 132
23* 11= اول ما نجمع الرقمين 2+3= 5 هذا نضعه بالمنتصف مابين 253
لهسه كلش تمام بس اذا طلع حاصل جمع الرقمين اكبر من 10
مثلا 67*11=737
يا جنه الطريقه ما نجحت بعد
لا لا هم تنجح بس اول ما نجمع الرقمين 6+7= 13ونخليه بالنصف ما بين 6 و 7
بس بما ان ما بين 6 و 7 مرتبه وحده اذا لازم انقل مرتبة العشرات من 13 واضعها على الي بعده وهي 6
فيصير1+6=7 اذا النتيجه 737
مثال اخر
85*11=
اول ما نجمع 8+5=13 اخذ الواحد من 13 واخليه على 8 تصير 9
اذا النتيجه 935
مثال اخر
39*11=
ناخذ 3+9 = 12 ناخذ ال1 من 12 ونخليه على 3 تصير 4
اذا النتيجه 429
مثال اخير اصعب
99*11=
ناخذ 9+9= 18 ناخذ ال1 ونخليه على على 9 تصير 10
اذا 1089
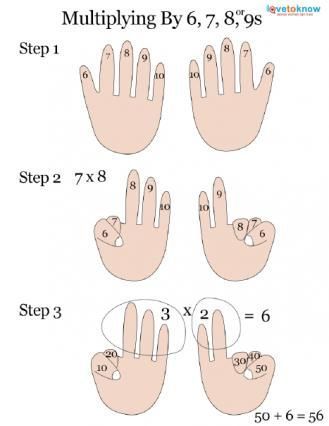
جدول الضرب لل 9 و8 و 7و 6 باستخدام صابيع اليدين
يعني اذا عدنا 5 في رقم او 3 في رقم ما اتنفع
الطريقه هيج
1- نتخيل لكل اصبع رقم نبدي من 6 الى 10 كما في الصوره
2- الرقم المضروب نحني صبعه الى الاسفل يعني اذا كلت 7 في رقم الاصبع الي يحمل رقم 7 احني مع الاصابع الي تسبقه واذا كلنا 8 في رقم نحني الاصبع الي يحمل رقم 8 مع الاصبع الي تسبقه
3- الارقام الواقفه نضربهن ابعض والارقام المنحنيه نجمعهن ونخلي الهن0 (بالحقيقه نضربهن في 10 ) بعدها نوضع الارقام جنب بعض
مثلا اذا عدنا 9 * 6
اولا نحني رقم 6
ثانيا نحني رقم 9 مع الاصابع الي قبله
ثالثا الاصابع الواقفه باليد الي فيه رقم 6 فقط 4 والاصابع الي واقفه باليد الي بيه 9 فقط واحد
رابعا نضرب 1* 4 = 4
خامسا الاصابع المنحنيه عددهن 1+4 = 5 اي 50
سادسا 50+4 = 54 والي هي نتيجه ضرب 9 * 6
لهنا لحكني الرياضياااات
مرحبا هاني... وعودة لمسألة المثلث السابقة ..
مع ان الحسابات التقليدية أدت الى نظام معادلات لانهائي الحلول
بس بقت سالفته مشكلة براسي.. أن كيف يمكن لشكل هندسي محدد الزوايا ان يعطي قيم زوايا متعددة !
بحثت عن المسألة بكوكل .. ووجدت ان احد المواقع يصفها على انها من ضمن المسائل السهلة الممتنعة جداً وعلى نص تعبيره
World's Hardest Easy Geometry Problem
وان حلها يتم بالخطوات الاتية ..

رائع صديقي هاني :)
اذا تحب نجمع البرمجة مع الرياضيات انا حاضر