التوابع الرياضية الخاصة في الماتلاب
أولاً : مقدمة ...
يتم التعامل مع كثيرات الحدود في الماتلاب من خلال توابع خاصة أعدت لحل كثيرات الحدود ضمن هذا البرنامج , حيث يتم تحويل كثير الحدود إلى شعاع سطري , وتمثل الأعداد ضمن هذا النسق معاملات كثير الحدود , وترتب ضمن النسق بشكل تنازلي يوافق قوى المتحول في كثير الحدود بدءاً من القوة (n) وحتى القوة (0) بما في ذلك المعاملات المعدومة للمتحول , حيث (n) أعلى رتبة للمتحول في كثير الحدود وذلك للتوافق ما الأسلوب الذي يتعامل معه برنامج الماتلاب في حل كثيرات الحدود.
مثال بسيط :
f(t) = 7t^4+6t^3+3t^2+t+5
يتم تمثيل كثير الحدود هذا بالمصفوفة :
ثانياً :العمليات الحسابية على كثير الحدود ...
·إيجاد جذور كثير حدود :
إن التابع roots هو التابع الخاص في الماتلاب الذي يمكن عن طريقه إيجاد جذور كثير حدود , حيث يعطي هذا التابع جذور كثير الحدود على شكل شعاع عمود وعناصر هذا الشعاع هي جذور كثير الحدود.
%f(t) = 7*t^4+6*t^3+3*t^2+t^1+5;
A = [7 6 3 1 5];
A_roots = roots(A)
%f(t) = 7t^3+5t^2-3t^1+10
A = [7 5 -3 10];
A_roots = roots(A)
·إيجاد كثير حدود انطلاقاً من جذوره :
باستخدام التابع الخاص poly يمكن إيجاد كثير حدود إنطلاقاً من جذوره , أي أن وظيفة هذا التابع معاكسة تماماً للتابع سابق الذكر.
A = [1 3 4 5 6];
roots(A)
poly(ans)
A = [3 5 6 7 8 9];
roots(A)
poly(ans)
نلاحظ من المثال الثاني أن هناك كثير حدود غير كثير الحدود الذي ادخلناه أولاً له نفس الجذور , وبالتالي ليس بالضرورة الحصول على التابع المدخل مسبقاً عند استدعاء (إعادة توليد) كثير الحدود الجديد من التابع (poly) , كمال هو جدير بالذكر أنه هذا تابع فيه نسبة خطأ لا تتجاوز (1/1000000) قد تظهر في بعض الحالات
·حساب قيمة كثير حدود عند قيمة معينة :
تتم هذه العملية في الماتلاب باستخدام التابع الخاص polyval(p,x) حيث يعبر p النسق (المصفوفة) الممثل لكثير الحدود , والرمز x يعبر عن قيمة المتحول المراد حساب كثير الحدود عنده.
G(x) = t^2+t+1
p = [1 1 1];
x = 3;
gx = polyval(p,x)
gx= 13
كما يمكن بطريقة ثانية إيجاد قيمة كثير الحدود لأجل قيمة معينة باستخدام التابع الخاص subs وبالاستعانة بالتعليمة syms حيث يقوم هذا الأخير بتحويل قيمة المتحول x إلى رمز يمكن التعامل معه من قبل البرنامج والتعرف عليه , والأمر subs الذي يقوم بحساب القيمة لكثير الحدود عند قيمة المتحول المطلوبة (أي أن التعليمة syms وظيفتها تعريف المتغير x)
syms x
gx = x^2 + x + 1;
subs(gx,3)
syms xy
gx = y*x^2 + x*y + 1;
subs(gx,x,3)
subs(gx,y,3)
المطلوب حساب قيم كثير الحدود من أجل عناصر المصفوفة x
p=[1 1 1]
x = [2 4 6]
gx = polyval(p,x)
·اشتقاق كثيرات الحدود :
يمكن إيجاد مشتق كثير حدود باستخدام التابع polyder وتكون النتيجة عبارة عن كثير حدود يمثل مشتق كثير الحدود الأصل.
gx = [2 5 -6 -5];
a = polyder(gx)
لمقارنة التابع مع مشتقه بيانياً , يمكن رسمهما معاً على نفس المحاور (محاور الاحداثيات) بالتعليمات التالية :
x=-10:0.5:10;
gx=[2 5 -6 -5];
a = polyder(gx)
plot(x,polyval(gx,x),'-*r',x,polyval(a,x),'-og')
كما يمكن استخدام مشتق كثير الحدود بطريقة أخرى وذلك باستخدام الأمر syms والأمر diff(function name) ...
syms x
gx = 2*x^3 + 5*x^2 - 6*x - 5;
diff(gx)
syms x
gx = 2*sin(2*x)*exp(x)
diff(gx)
ans = 4*cos(2*x)*exp(x) + 2*sin(2*x)*exp(x)
syms xy
gx = 2*sin(x*y)
diff(gx,x)
في هذا المثال نلاحظ أن التابع diff يمكنه أيضاً حساب المشتق بالنسبة لأحد المتحولات (في حال وجود أكثر من متحول في التابع , في مثالنا هذا قمنا بإيجاد مشتق التابع بالنسبة للمتحول (x).
كما يمكن أيضاً من خلال هذا التابع إيجاد المشتقات من المرتبة الثانية والثالثة ومافوق وذلك كما يلي
أي إيجاد المشتق (الثاني أو الثالث) بالنسبة للمتحول x....
·تكامل كثيرات الحدود :
من المعروف أن الاشتقاق هو عملية معاكسة للاشتقاق , ويمكننا التابع polyint الموجود في المكتبة الرياضية في الماتلاب من إيجاد تكامل تابع من خلال إدخال معاملات كثير الحدود بشكل نسق(مصفوفة) كما سبق في الأمثلة السابقة .
المطوب إيجاد تكامل كثير الحدود (6x2+10x-6) من أجل ثابت تكامل k = -5
p =[6 10 -6];
k = -5;
gx = polyint(p,k)
كما يمكن إيجاد تكامل كثير الحدود باستخدام syms والتابع int وذلك بشكل يماثل التابع diff لإيجاد المشتق ....
·إيجاد معادلة كثير الحدود الملائم :
إذا كان لديك مجموعة نقاط من منحني لا تعرف معادلته وتريد ان تشكل معادلة لهذا المنحني , فيمكن الاستعانة بالتابع polyfit للقيام بهذه العملية , حيث أنه يعطيك معادلة كثير الحدود الملائم للمنحني بحيث أنك تختار درجة كثير الحدود الذي تريد الحصول عليه.
x=[0:0.2:1.2];
y=[1 2 4 7 8 5 2];
u=polyfit(x,y,3)
t=polyval(u,x)
plot(x,y,'-or',x,t,'-*')
·العمليات الرياضية على كثيرات الحدود :
يمكن جمع وطرح كثيرات الحدود من خلال التعامل مع المصفوفات الممثلة لها مع ملاحظة ان تكون كلا المصفوفتين من نفس الدرجة والمثال التالي يوضح ذلك ....
A = 2x4 + x3 + 3x2 + x + 1
A = [2 1 3 1 1];
B = [4 -1 -1];
C = A + [0,0,B]
D = A - [0,0,B]
, (Convolution مختصر كلمة (convاما عملية الجداء فيمكن القيام بها بالاستعانة بالتابع
حيث باستخدام هذا التابع يتم الحصول على جداء كثيرات الحدود بشرط أن تعرف كثيرات الحدود بأنساق موافقة ومعبرة عن معاملاتها.
conv(A,B) %conv(B,A)
الجدول التالي يبين أهم التوابع المستخدمة وحسب الترتيب الأبجدي
|
|
|
|
اكتشاف معادلة كثير حدود جذورها معلومة |
|
|
|
|
|
|
|
حساب قيمة كثير الحدود عند قيمة معينة |
|
|
|
|
|
: المصدر
خطوات في احتراف الماتلاب دار شعاع -
كتاب البرمجة 3 منشورات جامعة دمشق -
----------------------------------------------------------------------------------------------------
§البرنامج الأول :
برنامج يبين فرق الطور بين الإشارات الجيبية
t=linspace(-1,1,101); مصفوفة متزايدة خطياً
x=2*cos(2*pi*t);
y=2*cos(2*pi*(t-0.125));
z=2*sin(2*pi*t);
plot(t,x,t,y,t,z)
axis([-1,1,-3,3])
title('Sinusoidal Signals')
ylabel('Amplitude')
xlabel('Time (s)')
text(-0.13,1.75,'x') تسمية كل شكل
text(-0.07,1.25,'y')
text(0.01,0.8,'z')
grid onتفعيل الشبكة
§البرنامج الثاني :
برنامج التمثيل الطوري للإشارة الجيبية أي رسم القسم الحقيقي بالنسبة للعقدي ورسم كل منهما بالنسبة للزمن ...
من المعلوم أن الإشارة الجيبية لها تمثيل عقدي يبين بالشكل التالي : = cos() + j.sin(
t=(-2e-03:0.02e-03:2e-03);
x=exp(j*2000*pi*t); exp التابع الأسي في الماتلاب
y=real(x); القسم الحقيقي للإشارة
z=imag(x);القسم الوهمي للإشارة (التخيلي)
subplot(2,1,1) تقسيم الرسم
plot(x,'-.k')
axis squareجعل المحاور مربعة الشكل
title('exp(jwt)')
xlabel('Real')
ylabel('Imaginary')
subplot(2,1,2)
plot(t,y,'-',t,z,':')
title('Re[exp(jwt)] and Im[exp(jwt)] vs t w=1000*2*pi')
xlabel('Time (s)')
grid on
legend('Re[exp(j\omegat)]','Im[exp(j\omegat)]',-1)
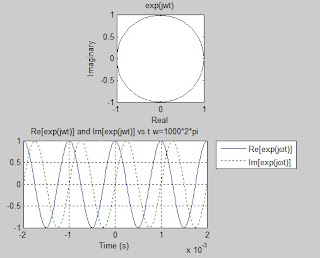
§البرنامج الثالث :
برنامج دمج نغمتين ...
t=linspace(-1e-2,1e-2,1001);
x=cos(2*pi*1500*t) + cos(2*pi*1300*t); نفس المطال,غير تردد
m=2*cos(2*pi*100*t);الإشارة المرجعية (إشارة الغلاف)
plot(t,m,'b:',t,-m,'b:',t,x,'k')
axis([-0.01 0.01 -2.4 2.4])
title('Beating between tones')
xlabel('Time (s)')
ylabel('Amplitude')
§البرنامج الرابع :
برنامج يمثل دخول الضجيج على الإشارة الجيبية ...
t=linspace(0,10,512)
s=sin(2*pi/5*t);الإشارة الأصلية
n=0.1*randn(size(t)); إشارة الضجيج
x = s + n;الإشارة المشوهة
disp('Signal to Noise Ratio(SNR), dB')
SNR = 20*log10(std(s)/std(n)) نسبة الإشارة إلى الضجيج
plot(t,x,'.',t,s,'r')
xlabel('Time (s)')
ylabel('Signal Amplitude')
title('Noisy signal')
استخدمنا في هذا البرنامج التابع std وتكمن وظيفة هذا التابع في حساب الانحراف المعياري.
§البرنامج الخامس :
برنامج لرسم الإشارة المقومة
t=linspace(0,10,512)
x=sin(t);
x1=x.*(x>0); الإشارة المقومة الأولى
x2=abs(x);الإشارة المقومة الثانية
subplot(3,1,1) تجزئة الرسم
plot(t,x)
xlabel('Time (s)')
ylabel('Amplitude')
title('continuous signal')
subplot(3,1,2)
plot(t,x1)
axis([0 10 -1.1 1.1])
title('Discontinuous signal')
xlabel('Time (s)')
ylabel('Amplitude')
subplot(3,1,3)
plot(t,x2)
axis([0 10 -1.1 1.1])
title('DC signal')
xlabel('Time (s)')
ylabel('Amplitude')
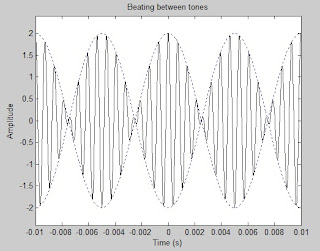
§البرنامج السادس :
برنامج لحساب المقاومة المكافئة لدارة مؤلفة من n ممانعة من الشكل(RjX) بحيث يحدد المستخدم عدد الممانعات الكلي في الدارة وقيمة كل ممانعة بقسميها الحقيقي والوهمي , كما يحدد المستخدم طريقة توصيل الممانعات بشكل تسلسلي أو تفرعي وبالتالي يكون المستخدم قد حدد شكل الدارة بالكامل...
يجب في هذا البرنامج ملاحظة أن الممانعة رقم n لا يهمني طريقة توصيلها ومايهمني هو طريقة توصيل الممانعة (n-1) معها ولذلك سنلاحظ أن البرنامج لن يسأل عن طريقة توصيل الممانعة n وإنما سيبدأ السؤال بالممانعة (n-1)
n = 8; فرضاً
P = ones(1,n);مصفوفة سطرية واحدية
for i=n:-1:1
P(1,i) = input (['Z' num2str(i) ':']); إدخال قيم الممانعات بالترتيب
end
Q = ones(1,n-1);
for j=1:n
if j==1
connect = input([' Z' num2str(n-j) ' series or Parallel : ']);
switch connect تحديد نوع توصيل الممانعات
case {'series''s'}
Q(1,n-1) = P(1,n) + P(1,n-j);
case {'Parallel''P'}
Q(1,n-1) = (P(1,n)*P(1,n-j))/(P(1,n)+P(1,n-j));
end
else
if n==j
break; إيقاف البرنامج عندما تصل الحلقة لقيمة مساوية لعدد الممانعات في الدارة
else
connect = input([' Z' num2str(n-j) ' series or Parallel : ']);
switch connect
case {'series''s'}
Q(1,n-j) = Q(1,n-j+1) + P(1,n-j);
case {'Parallel''P'}
Q(1,n-j) = Q(1,n-j+1)*P(1,n-j)/(Q(1,n-j+1)+P(1,n-j));
end
end
end
end
Zeq = Q(1,1); هذا العنصر من المصفوفة يمثل الممانعة الكلية المكافئة للدارة
تنفيذ البرنامج :
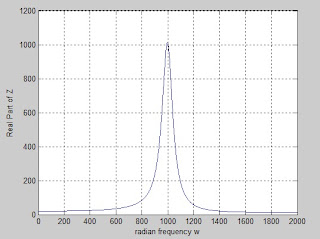
§البرنامج السابع :
w=0 2000;
2000;
z=(10+(10.^4-j.*(10.^6./(w)))./(10+j.*(0.1.*w-10.^5./w)));
Real=real(z);
plot(w,Real);
xlabel('radian frequency w');
ylabel('Real Part of Z');
grid on
pause(5)
imagine=imag(z);
plot(w,imagine);
grid on
xlabel('radian frequency w');
ylabel('Imaginary Part of Z');
§البرنامج الثامن :
برنامج لرسم تغيرات إشارة التوتر المتناوب V(t)=Asin(wt+alpha)+k مع الزمن.
f=50
Vm=110;
alpha=pi/6;
k=0.25*Vm;
T=1/f;
step=T/20;
t1=0
t2=3*T;
t=t1:step:t2;
V=Vm*sin(2*pi*f*t+alpha)+k;
fig=figure;
ax=axes;
set(ax,'xlim',[t1 t2],'ylim',[-200 200]);
title('V=Vm*sin(2*pi*f*t+alpha)+k');
xlabel('Time Axis (second)');
ylabel('Voltage Axis (Volt)');
hold on;
grid on;
ta=line([t1 t2],[0 0]);
set(ta,'color','r','linewidth',2);
Vo=line([t1 t2],[k k]);
set(Vo,'color','b','linestyle','-.');
plot(t,V,'r-*');
الجدول التالي يبين أهم الأوامر والتوابع في الماتلاب
|
|
القيمة المطلقة أو طويلة العدد العقدي |
|
|
|
الجواب عند حدم إسناد التعبير |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
إعطاء 15 مرتبة بعد الفاصلة العشرية |
|
إعطاء 15 مرتبة إضافية للقوة |
|
|
|
إعطاء 5 مراتب إضافية للقوة |
|
التحول إلى المستوي اللابلاسي |
|
|
|
|
|
تثبيت المخطط المرسوم على الشاشة |
|
|
|
|
|
|
|
|
|
|
|
|
|
اللوغاريتم الطبيعي (النبري) |
|
الرسم على محورين لوغاريتميين |
|
أخذ لوغاريتم عناصر مصفوفة |
|
|
|
|
|
|
|
|
|
القيمة المتوسطة التربيعية |
|
|
|
|
|
|
|
|
|
الرسم في المستوي الديكارتي |
|
|
|
|
|
توليد أعداد عشوائية أو مصفوفة |
|
|
|
|
|
|
|
|
|
رسم نصف لوغاريتمي \ المحور x هو اللوغاريتمي |
|
رسم نصف لوغاريتمي \ المحور y هو اللوغاريتمي |
|
|
|
|
|
|
|
رسم منحني الاستجابة الواحدية |
|
إدراج المتحولات الموجودة في الذاكرة |
|
الجدول التالي يبين أهم العمليات والعلاقات في الماتلاب
الجدول التالي يبين أهم الرموز الخاصة في الماتلاب
|
|
|
التعبير الرياضي عن الأشعة |
|
الفصل بين التعليقات وبين مناقشة الوظائف |
|
سطروإنهاء السطر ووقف الكتابة ومنع الأمر المنفذ قبلها من الظهور |
|
|
|
إشارة تدل على أن ما بعدها تعليق يهمله البرنامج |
المصدر :
- خطوات في احتراف الماتلاب - دار شعاع
- كتاب البرمجة 3 - منشورات جامعة دمشق
2000;






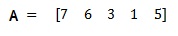



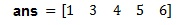

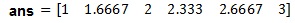
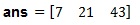
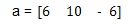












 رد مع اقتباس
رد مع اقتباس