أولاً : مقدمة ...
سنتعرض لدراسة أهم الأوامر التي تتعلق بالرسم ثنائي البعد في الماتلاب وطرق المعالجة والتنسيق للرسوم البيانية.
ثانياً : الخصائص الرئيسية للرسم البياني ثنائي البعد في الماتلاب ...
1.تعليمة الرسم الأساسية :
plot(Y)
plot(X1,Y1,….)
plot(X1,Y1,LineSpec,….)
plot(…,’PropertyName’,PropertyName,…)
plot(axes_handle,…)
h = plot(…)
hlines = plot(‘v6’,…)
ومن الخصائص الإضافية لهذه التعليمة أيضاً :
·LineWidth : تحديد عرض الخط (سماكة)
·MarkerEdgeColor : تحديد لون حواف العلامات المميزة
·MarkerFaceColor : تحديد لون العلامات المميزة
·MarkerSize : تحديد قياس العلامة المميزة
مثال :
ملاحظة : جميع التعليمات السابقة (داخل جسم plot) تكتب في سطر واحد.
ملاحظة : إعطاء قيم متقاربة للمتغير x يجعل دقة الرسم أعلى .
الجداول التالية توضح الرموز الدالة على الألوان والرموز الدالة على خطوط الرسم والرموز الدالة على نماذج العلام والمستخدمة في تعليمة الرسم جسم التابع plot والتي سنراها في أمثلة لاحقة.
اللون |
الرمز |
أخضر مزرق |
Cyan |
c |
ارجواني |
Magenta |
m |
أصفر |
Yellow |
y |
أسود |
Black |
k |
أزرق |
Blue |
b |
أحمر |
Red |
r |
أخضر |
Green |
G |
الرمز |
نموذج خط الرسم |
" – " |
|
" -- " |
-------------------------- |
none |
بدون خط رسم |
" : " |
.............................. |
"-." |
-.-.-.-.-.-.-.-.-.- |
الرمز |
الدلالة |
+ |
إشارة جمع |
O |
دائرة |
* |
نجمة |
. |
نقطة |
> |
مثلث رأسه لليمين |
< |
مثلث رأسه لليسار |
^ |
مثلث رأسه للأعلى |
وهناك أيضاً نماذج أخرى يمكن الإطلاع عليها من خلال أمر المساعدة إذا دعت الحاجة لها.
2.رسم منحنيين على شكل واحد :
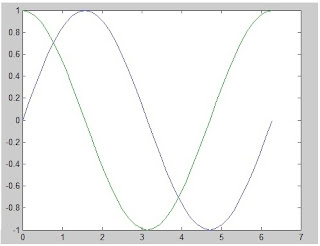
مثال (1) :
x = 0:0.05*pi:2*pi;
y = sin(x)
z = cos(x)
plot(x,y,x,z)
وبذلك نستطيع أن رسم عدد كبير من المنحنيات على نفس الشكل.
3.تسمية الشكل والمحاور :
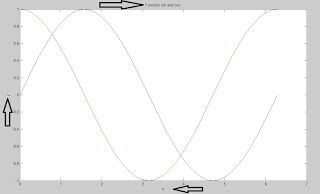
لو أضفنا الأسطر التالية على البرنامج السابق يصبح الرسم ...
title('Function sin and cos')
xlabel('x')
ylabel('y')
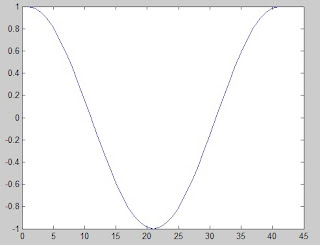
مثال (2) :
z = cos(x)
plot(z)
يأخذ التابع أول قيمة من التابع y ويأخذ x رقم العنصر أي كأنك كتبت : plot(1:length(z),z)أما لو كانت z عقدية فإنه يرسم القسم العقدي بالنسبة للقسم الحقيقي.
4.تلوين الأشكال :
الجدول الموضح في الأعلى يوضح رموز الألوان التي نريد الرسم فيها.
5.إنشاء شبكة :
إن الأمر grid on يعطيك شبكة حسب تقسيمات المحاور ولإزالة الشبكة مرة أخرى نكتب grid off .
6.الكتابة على الشكل :
نستطيع كتابة أي نص على الرسم وذلك بتحديد إحداثياته فقط : text(5,0.1,’sin’)
7.أبعاد المحاور :
إن البرنامج بشكل تلقائي يحدد لك أبعاد المحاور ولكن لو أردت تحديد هذه الحدود فإليك التعليمة التالية : axis([-15 15 -17 17]) إن أول رقمين يحددان مجال المحور x وثاني رقمين يحددان مجال المحور y.
8.تسمية كل منحني حسب لونه :
إذا كان لدينا شكل يحوي عدة توابع متداخلة وأردنا تعريف كل تابع حسب لونه أو غيره فيمكن استعمال التعليمة التالية :
legend(‘sin(x)’,’cos(x)’,’sin(x)./x’)
هذا الأمر سيأخذ لون الشكل الأول ويضع بجانبه أول عبارة تضعها في أمر legend والثاني مع الثاني وهكذا ...
ثالثاً : أمثلة عامة ...
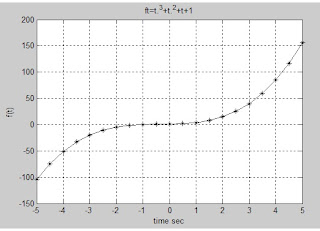
المثال الأول
برنامج لرسم تغيرات كثير الحدود f(t) =t.t.t + t.t + t + 1 مع تغيرات t.
t=-5:0.5:5;
ft=t.^3+t.^2+t+1;
plot(t,ft,'-*k');
grid on
title('ft=t.^3+t.^2+t+1');
xlabel('time sec');
ylabel('f(t)');
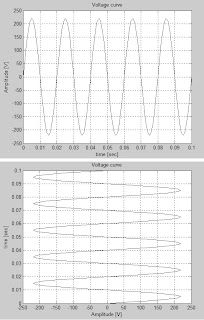
المثال الثاني
برنامج لرسم تغيرات التابع البسيط y = A sin(wt) مع تغيرات الزمن.
t=0:0.001:0.1;
A=220;
f=50;
w=2*pi*f;
y=A*sin(w*t);
plot(t,y,'k-')
title('Voltage curve');
xlabel('time [sec]');
ylabel('Amplitude [V]');
grid on;
pause
plot(y,t,'k-')
title('Voltage curve');
xlabel('Amplitude [V]');
ylabel('time [sec]');
grid on;
سبق وشرحنا عم التابع pause في درس سابق , حيث هذا التابع يقوم بإيقاف البرنامج حتى يضغط المستخدم أي زر ليتمم عمل البرنامج حتى نهايته , في مثالنا هذا يقوم البرنامج بعملية الرسم وفق العلاقة plot(t,y,’k-‘) وعندما يضغط المستخدم أي زر من لوحة المفاتيح فإن البرنامج سوف يحذف الرسم ليرسم وفقاً للعلاقة plot(y,t,’k-‘).
سأكتفي بهذا القدر بالنسبة للرسم ثنائي البعد في الماتلاب وسأدع الأمور الأخرى لك كي تتعلمها لوحدك وذلك بالاستعانة ببيئة الhelp المتوفرة في الماتلاب والتي تعد طريقة ممتازة للبحث تعلم الماتلاب , علماً ان برنامج الماتلاب يوفر إمكانية الرسم الثنائي البعد بالصيغة القطبية وبالصيغة العقدية ويوفر إمكانية الرسم على شكل أعمدة من أجل التطبيقات الإحصائية أو من أجل إظهار قيم التوافقيات في التوترات والتيارات في التطبيقات الهندسية , كما يمكننا البرنامج من الرسم على لوحة بأبعاد الرسم اللوغاريتمية.
: المصدر
خطوات في احتراف الماتلاب دار شعاع -
كتاب البرمجة 3 منشورات جامعة دمشق -
-------------------------------------------------------------------------------------------------------------------------
يحوي الماتلاب العديد من التوابع لعرض وتمثيل البيانات بالرسم ثلاثي البعد, إما بهيئة خطوط ثلائية البعد أو بأنواع مختلفة من السطوح.
1) plot3
ولكنه يؤمن الرسم ثلاثي البعد , يكتب هذا التابع بالصيغة plot إن هذا التابع مشابه للتابع
plot3(x, y, z)
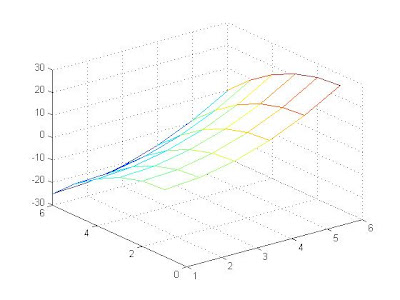
2) mesh Surfaces
: لنأخذ المثال التالي من أجل رسم التابع
z=x^2 - y^2
سنحصر الرسم ليكون فقط في الربع الأول من الإحداثيات بحيث سنجعل
0 <= x <= 5
0<= y <= 5
:من أجل ذلك نكتب
[x y]=meshgrid(0:5);
z=x.^2-y.^2;
mesh(z)
:كما هو مكتوب بالأعلى يولد المصفوفتين التاليتين meshgrid إن التابع
x=[0 1 2 3 4 5;0 1 2 3 4 5;0 1 2 3 4 5;0 1 2 3 4 5;0 1 2 3 4 5;0 1 2 3 4 5];
y=[0 0 0 0 0 0;1 1 1 1 1 1;2 2 2 2 2 2;3 3 3 3 3 3;4 4 4 4 4 4;5 5 5 5 5 5];
: وبالنتيجة نحصل على الشكل
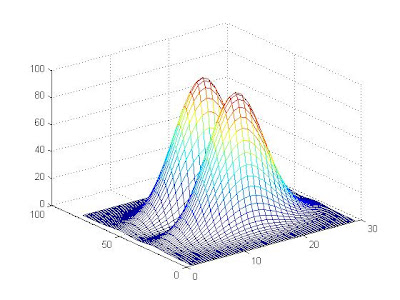
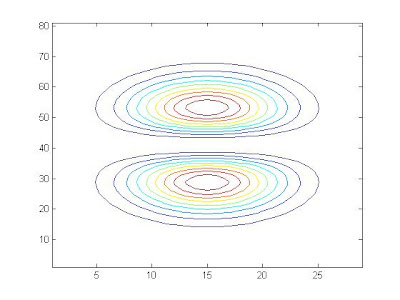
3) Contour plots
:لنأخذ المثال التالي
[x,y]=meshgrid(-2.1:0.15:2.1,-6:0.15:6);
u=80*y.^2.*exp(-x.^2-0.3*y.^2);
mesh(u)
pause
contour(u)
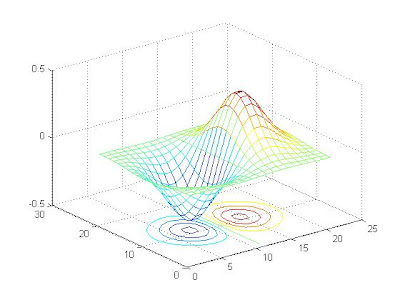
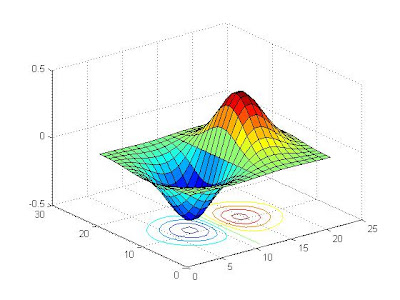
4) meshc plot
: لنأخذ المثال التالي
[x,y]=meshgrid(-2:0.2:2);
u=x.*exp(-x.^2-y.^2);
meshc(u)
pause
surfc(u)
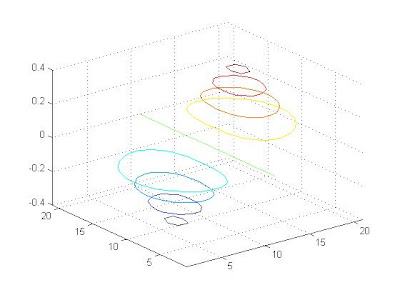
pause
contour3(u)
:المصدر
Essential MATLAB For engineering and Scientists








 رد مع اقتباس
رد مع اقتباس

