هنا

[Suzana]

النمذجة والمحاكاة للآلات الكهربائية
Electric Machines
الجزء الأول

النمذجة هي وضع النموذج الرياضي للنظام المدروس.
المحاكاة هي وضع المخطط الصندوقي المقابل للنموذج الرياضي للنظام المدروس.


أولاً : التحويلات ثلاثية الطور ...
في دراسة النظم الكهربائية , فإن التحويلات الرياضية غالباً ماتستخدم من أجل فك الترابط بين المتغيرات , وذلك من أجل تسهيل حل المعادلات المعقدة المتغيرة مع الزمن أو الانتقال إلى أساس مرجعي لكافة المتغيرات.
فلو أخذنا نظرية المركبات المتناظرة كمثال سنلاحظ أن التحويل العقدي يستخدم لتفكيك الترابط بين الأطوار (a,b,c) والحصول على المركبات :



حيث f [IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image003.png[/IMG] قد تكون تيار أو توتر أو سيالة ..... إلخ
ومصفوفة التحويل تعطى :

1- تحويل كلارك
إن الطورين الثابتين (المستقرين) في تحويل كلارك يتغيران ويرمز لهما بالشكل بالرمزين (alpha,beta).

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image009.png[/IMG]

الشكل المبين يوضح المحاور (a,b,c) وعلاقتها مع المحورين (alpha,beta) حيث نلاحظ انطباق المحور alpha[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image010.png[/IMG] مع الطور الأول ولكن المحور beta[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image011.png[/IMG] يتأخر عنه بزاوية 90 أما المركبة الثالثة فتعرف بالمركبة الصفرية

2- تحويل بارك
تحويل بارك معروف كثيراً في التحويل من نظام الأطوار الثلاثة إلى نظام الطورين في تحليل الآلات التزامنية , ومعادلة التحويل تعطى بالصيغة :

حيث يستخدم تحويل بارك من الانتقال بالكميات الثابتة للآلة التزامنية من المحاور ثلاثية الطور إلى نظام المحورين (d,q) والثابتة نسبة للدائر.
بعض المراجع تعتبر المحور q متأخر عن المحور d بزاوية 90 كما وضحنا , وهناك أخرين يعتبرون أن المحور q متقدم عن المحور d بزاوية 90 ويمكن التعامل مع التحويل كتابع للزاوية (theta(q [IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image024.png[/IMG] والشكل التالي يوضح ذلك

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image025.png[/IMG]

إن العلاقة بين (theta(d),theta(q)) كما تعرف في تحويل بارك هي : [IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image033.png[/IMG]



وبالتالي :

وبالتالي نلاحظ أن كلا التحويلين متشابهين تماماً ماعدا ترتيب المحاور (d,q).


مثال :
ارسم المخطط الصندوقي المقابل للمعادلات التالية :

طريقة أولى :
نحتاج في هذه الطريقة إلى :
- منبع جيبي متناوب.
- عناصر تضخيم (Gain)
- مازج (Mux)
- عنصر إظهار للنتائج (Scope)
والشكل التالي يبين المخطط الصندوقي (t=0.05 – f=50Hz – Ampliture = 5)

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image040.png[/IMG]

طريقة ثانية :
- منبع جيبي متناوب.
- مازج Mux و Demux (عكس المازج(
- عنصر تكبير (Gain) ولكن هنا نختار من خصائصه من

Multiplication à Matrix(k*u)

حيث k مصفوفة ثابتة بدلاً من ثابت (عنصر)



[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image041.png[/IMG]
طريقة ثالثة :
ملاحظة : لابد في هذه الطريقة من الانتباه أن المصفوفة المدخلة في عناصر التضخيم مختلفة عن الطريقة السابقة وذلك لأنه يتم التعامل مع كل طور على حدى مع المحاكاة.

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image042.png[/IMG]

طريقة رابعة :



من أجل التأكد من أن النتائج متطابقة تماماً بكل الطرق ما علينا إلا دمج نتائج الحالات الأربعة باستخدام عنصر (Mux) ومن ثم إظهارها على راسم وفي حال تطابق جميع النتائج فلن يظهر لنا إلا ثلاثة أشكال مزاحة عن بعضها بزاوية 120 , والشكل التالي يوضح ذلك

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image044.png[/IMG]

: المرفقات على الرابط
http://www.mediafire.com/?rwr6ev68w8b1vnx


: المصدر
Dynamic Simulation of Electric Machinery Using MATLAB/Simulink
محاضرات النمذجة والمحاكاة - الدكتور علي الجازي

[Suzana]

النمذجة والمحاكاة للآلات الكهربائية
Electric Machines

الجزء الثاني
المحولات الكهربائية أحادية الطور





سنبدأ باستنتاج معادلات السيالة المغناطيسية (التشابك المغناطيسي) والتوتر على أطراف المحولة ذات الملفين (ابتدائي وثانوي) , آخذين بعين الاعتبار المقاومة والسيالة التسربية للملفات والممانعة المغناطيسية للنواة , ومن ثم سنستنتج الدارة المكافئة التي تمثل المحولة.


1- معادلات السيالة والتشابك في المغناطيسي بين الملفات في المحول
تتكون السيالة المغناطيسية في كل ملف من ملفات المحولة من جزأين إذا ما تم أخد السيالة التسربية بعين الاعتبار , كما يبين الشكل

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image001.png[/IMG]

الشكل الموضح يبين مسارات الفيوض في المحول أحادي الطور. والشكل التالي يوضح المخطط التمثيلي للمحول أحادي الطور.



حيث تتكون السيالة الكلية من مركبتين حيث المركبة الأولى تمثل السيالة المتبادلة وهي متساوية لكلا الملفين (هي السيالة التي تربط بين الملفين) والمركبة الثانية تمثل السيالة التسربية الخاصة بكل ملف.

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image003.png[/IMG]

ينشأ الفيض المتبادل في المحول المثالي من القوة المحركة المغناطيسية للملفين والذي يدور بنفس المسار في النواة. بفرض أن [IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image007.png[/IMG] هو عدد لفات الملف الأول (الابتدائي) , يربط فعلياً كل من الفيض المتبادل والفيض المتسرب , فإن التشابك المغناطيسي في الملف الأول (الابتدائي) يحدد بأنه عدد لفات الملف الابتدائي مضروباً بالتدفق الكلي الناتج عن الملف الأول :

ويمكن ان يعبر عن الطرف الأيمن للمعادلة الأخيرة بدلالة تيارات الملفات , باستبدال الفيض المتبادل والفيض المتسرب بالقوى المحركة المغناطيسية والمسايرات الخاصة بهذه الملفات. الفيض المتسرب في الملف الأول تسببه القوى المحركة المغناطيسية الناتجة عن الملف الأول والفيض المتبادل يسببه مجموع القوى المحركة المغناطيسية , وبالتعويض عن الفيض المتبادل والفيض التسربي بالمعادلة الأخيرة نجد :



2- معادلات التوتر
إن التوتر المتحرض في كل ملف يساوي إلى معدل تغير التشابك المغناطيسي ولذلك يمكن أن يعطى التوتر المتحرض في الملف الأول (الابتدائي) بالعلاقة التالية :

ومعادلات التوتر تكون كالتالي :

3- الدارة المكافئة لمحولة أحادية الطور
إن شكل معادلات التوتر المبين يحدد شكل الدارة المكافئة لمحولة ثنائية الملفات وذلك كما يبين الشكل التالي , إن إشارة الفتحة (') تدل أن قيم الثانوي منسوبة إلى الطرف الأولى (الابتدائي) . إن قيم محددات الدارة للملف الثانوي منسوبة للأولي تحدد بالعلاقة :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image045.png[/IMG]


4- نمذجة المحولة أحادية الطور
من أجل نمذجة المحولة أحادية الطور (معرفة تغييرات مجاهيل بارمترات المحولة بالاعتماد على القيم المعلومة فيها) نحتاج إلى المعادلات التالية :

نستنتج أن مجموع المعادلات الأخيرة تشكل النموذج الديناميكي الأساسي لمحول ذي ملفين أولي وثانوي وهذه المعادلات غير مستقلة خطياً من حيث التشابك المغناطيسي ويمكن إضافة المفاقيد الحديدية لها إذا دعت الضرورة. وعند تنفيذ ملف المحاكاة يجب الأخذ بعين الاعتبار لما يلي :
- التشابك المغناطيسي كمتغيرات داخلية.
- توترات الأطراف هي معطيات الدخل المطلوبة.
- تيارات الملفات معطيات الخرج الرئيسية.
والمخطط التالي يدعى بالمخطط الانسيابي لعملية النمذجة لمحول بملفين (أحادي الطور) ...

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image055.jpg[/IMG]

ونموذج المحاكاة المقابل لهذا المخطط مبين بالشكل التالي ...



[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image056.png[/IMG]


يجب الانتباه دوماً بالقيام بربط المخطط الصندوقي مع ملف M-file لتعريف كافة المجاهيل (في المخطط) داخل الملف , ويجب تشغيل الملف أولاً وإدخال قيم العناصر المطلوبة ومن ثم تشغيل النموذج المقابل لهذا الملف.
بالنسبة للمخطط السابق يمكن مشاهدة المنحنيات (لكن لابد من الانتباه أن الدخل في هذا النموذج له قيمة ثابتة وليست متغيرة مع الزمن وكذلك الجهد الثاني له علاقة بالحمل غير الموجود) من خلال تنفيذ النموذج التالي :



[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image057.png[/IMG]


مثال (1) :
في النموذج السابق رأينا الحالة العامة لمخطط المحولة أحادية الطور , ولكن قيمة توتر الخرج يحددها الحمل وسنناقش في هذا المثال اختبارات المحولة الثلاثة (القصر – اللاحمل – التحميل) وذلك من خلال جعل المستخدم يحدد قيمة مقاومة الحمل ومن ثم يشاهد المنحنيات الناتجة عن قيمة الحمل التي قام بتحديدها , وذلك من أجل محولة لها المواصفات التالية :
S = 1500 VA – V = 120 Volt – f = 60 Hz – N = 0.5 – r1= 0.25 – r2'= 0.134
Xl1 = 0.056 – xl2' = 0.056
في هذا المثال لو جعلنا قيمة مقاومة الحمل مساوية للصفر سنكون قد اجرينا اختبار القصر على المحولة وستكون المنحنيات الناتجة ممثلة للمحولة أحادية الطور في حالة القصر أما لو جعلنا قيمة الحمل كبيرة جداً (100Zb) وأكبر فإن الاختبار المقابل لهذه الحالة هو اختبار اللاحمل ويمكن إجراء حالة التحميل الإفتراضية بإعطاء قيم مناسبة للحمل.
في هذا المثال لن نهمل أثر التشبع وسندخل حلقة خاصة بحالة التشبع في مخطط نمذجة المحولة وسندخل قيم تغيرات الفيض (السيالة) ضمن ملف القراءة وستتم معالجته من خلال العنصرLook-up table الذي سنراه في نموذج المحاكاة .
والبرنامج الذي يجب كتابته في ملف التحرير موضح كالتالي :


% محولة ذات ملفين


clear all % حذف كافة المتغيرات في الذاكرة


% تحديد بارامترات الدارة المكافئة للمحولة وكذلك منحني المغنطة


Vrated = 120; % الجهد
Srated = 1500; % الاستطاعة الظاهرية
Frated = 60; % التردد
Zb = Vrated^2/Srated; % ممانعة الأساس
wb = 2*pi*Frated; % تردد الأساس
Vpk = Vrated*sqrt(2); القيمة العظمى للجهد
NpbyNs = 120/240; % نسبة التحويل للمحول
r1 = 0.25; % مقاومة الأولي
rp2 = 0.134; % مقاومة الثانوي منسوبة للأولي
xl1 = 0.056; % المفاعلة التسريبية للأولي
xpl2 = 0.056; % المفاعلة التسريبية للثانوي منسوب للأولي
xm = 708.8; % المفاعلة المغناطيسية
xM = 1/(1/xm + 1/xl1 + 1/xpl2);






% منحني المغنطة المقابل للمصفوفتين التاليتين


Dpsi=[ -2454.6 -2412.6 -2370.5 -2328.5 -2286.4 -2244.4 -2202.3 ...
-2160.3 -2118.2 -2076.1 -2034.1 -1992.0 -1950.0 -1907.9 -1865.9 ...
-1823.8 -1781.8 -1739.7 -1697.7 -1655.6 -1613.6 -1571.5 -1529.5 ...
-1487.4 -1445.3 -1403.3 -1361.2 -1319.2 -1277.1 -1235.1 -1193.0 ...
-1151.0 -1108.9 -1066.9 -1024.8 -982.76 -940.71 -898.65 -856.60 ...
-814.55 -772.49 -730.44 -688.39 -646.43 -604.66 -562.89 -521.30 ...
-479.53 -438.14 -396.75 -355.35 -313.96 -272.56 -231.17 -192.60 ...
-154.04 -116.41 -81.619 -46.822 -19.566 0.0000 0.0000 0.0000 0.0000 ...
0.0000 0.0000 19.566 46.822 81.619 116.41 154.04 192.60 231.17 ...
272.56 313.96 355.35 396.75 438.14 479.53 521.30 562.89 604.66 ...
646.43 688.39 730.44 772.49 814.55 856.60 898.65 940.71 982.76 ...
1024.8 1066.9 1108.9 1151.0 1193.0 1235.1 1277.1 1319.2 1361.2 ...
1403.3 1445.3 1487.4 1529.5 1571.5 1613.6 1655.6 1697.7 1739.7 ...
1781.8 1823.8 1865.9 1907.9 1950.0 1992.0 2034.1 2076.1 2118.2 ...
2160.3 2202.3 2244.4 2286.4 2328.5 2370.5 2412.6 2454.6 ];


psisat=[ -170.21 -169.93 -169.65 -169.36 -169.08 -168.80 -168.52 ...
-168.23 -167.95 -167.67 -167.38 -167.10 -166.82 -166.54 -166.25 ...
-165.97 -165.69 -165.40 -165.12 -164.84 -164.56 -164.27 -163.99 ...
-163.71 -163.43 -163.14 -162.86 -162.58 -162.29 -162.01 -161.73 ...
-161.45 -161.16 -160.88 -160.60 -160.32 -160.03 -159.75 -159.47 ...
-159.18 -158.90 -158.62 -158.34 -157.96 -157.39 -156.83 -156.07 ...
-155.51 -154.57 -153.62 -152.68 -151.74 -150.80 -149.85 -146.08 ...
-142.31 -137.60 -130.06 -122.52 -107.44 -84.672 -42.336 0.0000 ...
0.0000 42.336 84.672 107.44 122.52 130.06 137.60 142.31 146.08 ...
149.85 150.80 151.74 152.68 153.62 154.57 155.51 156.07 156.83 ...
157.39 157.96 158.34 158.62 158.90 159.18 159.47 159.75 160.03 ...
160.32 160.60 160.88 161.16 161.45 161.73 162.01 162.29 162.58 ...
162.86 163.14 163.43 163.71 163.99 164.27 164.56 164.84 165.12 ...
165.40 165.69 165.97 166.25 166.54 166.82 167.10 167.38 167.67 ...
167.95 168.23 168.52 168.80 169.08 169.36 169.65 169.93 170.21 ];




% تحديد بارامترات المحاكاة
tstop = 0.2; % زمن التنفيذ
Psi1o = 0; % قيم ابتدائية
Psip2o = 0; % قيم ابتدائية


repeat_run = 'Y'; % لتكرار البرنامج أكثر من مرة
while repeat_run == 'Y'


disp('Enter value of RH, the high-gain resistor to develop v2''')
RH = input('Enter ohmic value of high gain resistor : ')
disp('')
disp('Run simulation then type ''return '' for plots')
keyboard
clf;
subplot(3,1,1)
plot(y(:,1),y(:,2),'-')
ylabel('v1 in V')
title('primary voltage')
subplot(3,1,2)
plot(y(:,1),y(:,3),'-')
ylabel('v2'' in V')
title('secondary voltage')
subplot(3,1,3)
plot(y(:,1),y(:,4),'-')
ylabel('psim in Wb/sec')
title('mutual flux')


h2=figure;
clf;
subplot(3,1,1)
plot(y(:,1),y(:,5),'-')
ylabel('i1 in A')
title('primary current')
subplot(3,1,2)
plot(y(:,1),y(:,6),'-')
ylabel('i2'' in A')
xlabel('Time in sec')
title('secondary current')


disp('Save plots before typing return')
keyboard
close (h2)


% تكرار البرنامج
repeat_run = input('Repeat with new system condition? Y/N: ','s');
if isempty(repeat_run) % رفض التكرار
repeat_run = 'N';
end
end % إنهاء الحلقة






[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image058.png[/IMG]
نتائج المحاكاة


حالة القصر

حالة اللاحمل

حالة التحميل








: المصدر
Dynamic Simulation of Electric Machinery Using MATLAB/Simulink
محاضرات النمذجة والمحاكاة - الدكتور علي الجازي

[Suzana]

--------------------------

النمذجة والمحاكاة للآلات الكهربائية
Electric Machines

الجزء الثالث
المحولات الكهربائية ثلاثية الطور



1) التوصيل نجمي – نجمي
في هذه الحالة يتم تأريض نقطة النجمة في الملف الابتدائي بمقاومة أما نقطتا النجمة للثانوي والمنبع تؤرضان مباشرة إلى الأرض , كما أن توتر نقطة الحيادي للابتدائي يكون عائماً من وجهة نظر تأريض النظام وذلك لأن التأريض غير مباشر.





الشكل التالي يبين مخطط التوصيل نجمي – نجمي لمحول ثلاثي الطور

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image013.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image014.png[/IMG]

2) التوصيل مثلثي – نجمي
في هذه الحالة يتم تأريض نقطة الحيادي في الثانوي بمقاومة , وتكون نسبة ملفات الثانوي إلى الابتدائي مساوية لجذر 3 مضروب بنسبة التحويل.






الشكل التالي يبين مخطط التوصيل مثلثي – نجمي لمحول ثلاثي الطور








…Simulink…



[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image035.png[/IMG]
…M-File…


% محولة ثلاثية الطور
% جميع البارمترات من أجل محولة ذات ملفين


clear all;




Vrated = 120; % rms rated voltage
Srated = 1500; % rated VA
Frated = 60; % rated frequency in Hz
Zb = Vrated^2/Srated; % base impedance
wb = 2*pi*Frated; % base frequency
Vpk = Vrated*sqrt(2); % peak rated voltage
NpbyNs = 120/240; % nominal turns ratio
r1 = 0.25; % resistance of wdg 1 in ohms
rp2 = 0.134; % referred resistance of wdg 2 in ohms
xl1 = 0.056; % leakage reactance of wdg 1 in ohms
xpl2 = 0.056; % leakage reactance of wdg 1 in ohms
xm = 708.8; % unsaturated magnetizing reactance in ohms
xM = 1/(1/xm + 1/xl1 + 1/xpl2);


% mag. curve Dpsi versus psisat


Dpsi=[ -2454.6 -2412.6 -2370.5 -2328.5 -2286.4 -2244.4 -2202.3 ...
-2160.3 -2118.2 -2076.1 -2034.1 -1992.0 -1950.0 -1907.9 -1865.9 ...
-1823.8 -1781.8 -1739.7 -1697.7 -1655.6 -1613.6 -1571.5 -1529.5 ...
-1487.4 -1445.3 -1403.3 -1361.2 -1319.2 -1277.1 -1235.1 -1193.0 ...
-1151.0 -1108.9 -1066.9 -1024.8 -982.76 -940.71 -898.65 -856.60 ...
-814.55 -772.49 -730.44 -688.39 -646.43 -604.66 -562.89 -521.30 ...
-479.53 -438.14 -396.75 -355.35 -313.96 -272.56 -231.17 -192.60 ...
-154.04 -116.41 -81.619 -46.822 -19.566 0.0000 0.0000 0.0000 0.0000 ...
0.0000 0.0000 19.566 46.822 81.619 116.41 154.04 192.60 231.17 ...
272.56 313.96 355.35 396.75 438.14 479.53 521.30 562.89 604.66 ...
646.43 688.39 730.44 772.49 814.55 856.60 898.65 940.71 982.76 ...
1024.8 1066.9 1108.9 1151.0 1193.0 1235.1 1277.1 1319.2 1361.2 ...
1403.3 1445.3 1487.4 1529.5 1571.5 1613.6 1655.6 1697.7 1739.7 ...
1781.8 1823.8 1865.9 1907.9 1950.0 1992.0 2034.1 2076.1 2118.2 ...
2160.3 2202.3 2244.4 2286.4 2328.5 2370.5 2412.6 2454.6 ];


psisat=[ -170.21 -169.93 -169.65 -169.36 -169.08 -168.80 -168.52 ...
-168.23 -167.95 -167.67 -167.38 -167.10 -166.82 -166.54 -166.25 ...
-165.97 -165.69 -165.40 -165.12 -164.84 -164.56 -164.27 -163.99 ...
-163.71 -163.43 -163.14 -162.86 -162.58 -162.29 -162.01 -161.73 ...
-161.45 -161.16 -160.88 -160.60 -160.32 -160.03 -159.75 -159.47 ...
-159.18 -158.90 -158.62 -158.34 -157.96 -157.39 -156.83 -156.07 ...
-155.51 -154.57 -153.62 -152.68 -151.74 -150.80 -149.85 -146.08 ...
-142.31 -137.60 -130.06 -122.52 -107.44 -84.672 -42.336 0.0000 ...
0.0000 42.336 84.672 107.44 122.52 130.06 137.60 142.31 146.08 ...
149.85 150.80 151.74 152.68 153.62 154.57 155.51 156.07 156.83 ...
157.39 157.96 158.34 158.62 158.90 159.18 159.47 159.75 160.03 ...
160.32 160.60 160.88 161.16 161.45 161.73 162.01 162.29 162.58 ...
162.86 163.14 163.43 163.71 163.99 164.27 164.56 164.84 165.12 ...
165.40 165.69 165.97 166.25 166.54 166.82 167.10 167.38 167.67 ...
167.95 168.23 168.52 168.80 169.08 169.36 169.65 169.93 170.21 ];


% set up simulation parameters
tstop = 1.2; % stop time
Psi1o = 0; % initial value of wdg l flux linkage
Psip2o = 0; % initial value of wdg 2 flux linkage
Rload = 120^2/1500 % referred impedance to primary side of
% the 1.5 kVA, unity power factor load
% connected across each secondary winding


repeat_run = 'Y'; % set up repeat run flag
while repeat_run == 'Y'


Rn = input('Enter ohmic value of neutral to ground resistor Rn > ');
disp('Run simulation and return for plots')
keyboard
clf;
subplot(4,1,1)
plot(y(:,1),y(:,2),'-')
ylabel('vAB in V')
title('primary line voltage')
subplot(4,1,2)
plot(y(:,1),y(:,3),'-')
ylabel('vab in V')
title('secondary line voltage')
subplot(4,1,3)
plot(y(:,1),y(:,4),'-')
ylabel('iA in A')
title('primary line current')
subplot(4,1,4)
plot(y(:,1),y(:,5),'-')
ylabel('ia in A')
title('secondary line current')
h2=figure;
subplot(4,1,1)
plot(y(:,1),y(:,6),'-')
ylabel('(iAB+iBC+iCA)/3 in A')
subplot(4,1,2)
plot(y(:,1),y(:,7),'-')
ylabel('(ia+ib+ic)/3 in A')
subplot(4,1,3)
plot(y(:,1),y(:,8),'-')
ylabel('vnG in V')
title('Secondary neutral to ground voltage')
xlabel('Time in sec')
disp('Save plots before typing return')
keyboard
close(h2)


% prompt for repeat with new system condition
repeat_run = input('Repeat with new system condition? Y/N: ','s');
if isempty(repeat_run) % if empty return a No to terminate
repeat_run = 'N';
end


end % while repeat_run


نتائج المحاكاة :





: المصدر
Dynamic Simulation of Electric Machinery Using
MATLAB/Simulink

[Suzana]

Electric Machines

الجزء الرابع
نمذجة آلات التيار المتناوب
المحرك التحريضي



سنناقش للمحرك التحريضي المواضيع التالية :
- مميزات المحرك التحريضي (خصائص التشغيل) }سرعة - تيار , سرعة - عزم , سرعة استطاعة و سرعة - مردود{.
- إقلاع وكبح المحركات التحريضية.
- سنناقش أيضاً بعض حالات المحرك التحريضي في حال وجود ممانعة بين نجمي ثابت المحرك التحريضي ونجمي الشبكة.
- المحرك التحريضي أحادي الطور.


الانتقال من نظام المحاور (a,b,c) لنظام المحاور المتعامدة (d,q) }تحويل بارك{
إن الغاية من الانتقال بين المستويات هو :
1- التخلص من التداخل بين كافة بارامترات المحرك التحريضي.
2- تقليل عدد المعادلات الواصفة للنظام وبالتالي تسهيل الحسابات.
ملاحظة : عملية النسب يمكن أن تكون لثابت المحرك أو للدائر....


- مصفوفة التحويل بين المحاور ....



لو جعلنا قيمة (theta=0 [IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image007.png[/IMG]) فإن هذه الزاوية ستعطيني في كل لحظة قيمة الزاوية للسيالة الدوارة على المحور المباشر (d) المفروض وتصبح المصفوفة ....



نموذج الماتلاب الواصف لهذه المصفوفة :





[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image011.png[/IMG]
النتائج :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image012.png[/IMG]

نلاحظ من النتائج أن المركبة الصفرية معدومة (في حالات العمل النظامية - المستقرة) تقريباً ولذلك يتم إهمال هذه المركبة في الحسابات.


كما أننا يمكننا العودة من نموذج المحاور (d,q) إلى النموذج ثلاثي الطور وذلك كمايبين النموذج التالي ....



[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image013.png[/IMG]
والمصفوفة الناتجة بالنتيجة تكون كما بالشكل :





نمذجة ومحاكاة المحرك التحريضي Simulation of An Induction motor in the Stationary Reference Frame

والشكل التالي يبين نموذج المحاكاة باستخدام الماتلاب ......

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image150.png[/IMG]

من الشكل نلاحظ أن نموذج محاكاة المحرك التحريضي يحوي العديد من النماذج الفرعية (Subsystem) وقد قم بترقيم كل منهم كما هو مبين ومحتوى كل منها مبين بالأشكال التالية ...

الصندوق (1)
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image151.png[/IMG]

الصندوق (2)
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image152.png[/IMG]



الصندوق (3)
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image153.png[/IMG]

الصندوق (4)

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image154.png[/IMG]



الصندوق (5)


[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image155.png[/IMG]

الصندوق (6)

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image156.png[/IMG]

…Script File… P1


Sb = 750; % rating in VA
Prated = 750; % output power in W
Vrated = 200; % rated line to line voltage in V
pf = 0.8;
Irated = Sb/(sqrt(3)*Vrated*pf); % rated rms current
P = 4; % number of poles
frated = 60; % rated frequency in Hz
wb = 2*pi*frated; % base electrical frequency
we = wb;
wbm = 2*wb/P; % base mechanical frequency
Tb = Sb/wbm; % base torque
Zb = Vrated*Vrated/Sb; %base impedance in ohms
Vm = Vrated*sqrt(2/3); % magnitude of phase voltage
Vb = Vm; % base voltage
Tfactor = (3*P)/(4*wb); % factor for torque expression


rs = 3.35; % stator resistance in ohms
xls = 6.94e-3*wb;% stator leakage reactance in ohms
xplr = xls; % rotor leakage reactance
xm = 163.73e-3*wb; %stator magnetizing reactance
rpr = 1.99; % referred rotor wdg resistance in ohms
xM = 1/(1/xm + 1/xls + 1/xplr);
J = 0.1; % rotor inertia in kg m2
H = J*wbm*wbm/(2*Sb); % rotor inertia constant in secs.
Domega = 0; % rotor damping coefficient


…Script File… m


% Load three-phase induction motor parameters from this File ....
p1 % load motor parameters from p1.m
% initialize to start from standstill with machine unexcited


Psiqso = 0; % stator q-axis total flux linkage
Psipqro = 0; % rotor q-axis total flux linkage
Psidso = 0; % stator d-axis total flux linkage
Psipdro = 0; % rotor d-axis total flux linkage
wrbywbo = 0; % pu rotor speed
tstop = 2; % use 2 sec simulation time for Fig. in text


% program time and output arrays of repeating sequence signal for Tmech


tmech_time = [0 0.8 0.8 1.2 1.2 1.6 1.6 tstop];
tmech_value = [0 0 -0.5 -0.5 -1. -1. -0.5 -0.5]*Tb;


% Transfer to keyboard for simulation
disp('Set up for running s1.m or s3.m');
disp('Perform simulation then type return for plots');
keyboard
clf;
subplot(4,1,1)
plot(y(:,1),y(:,2),'-')
ylabel('vag in V')
title('stator phase to neutral voltage')
subplot(4,1,2)

plot(y(:,1),y(:,3),'-')
ylabel('ias in A')
axis([-inf inf -25 25]);
title('stator current')
subplot(4,1,3)
plot(y(:,1),y(:,5),'-')
ylabel('Tem in Nm')
title('developed torque')
subplot(4,1,4)
plot(y(:,1),y(:,4),'-')
axis([-inf inf 0 1.2]);
ylabel('wr/wb')
xlabel('time in sec')
title('pu rotor speed')


المصدر :
Dynamic Simulation of Electric Machinery Using MATLAB/Simulink محاضرات النمذجة والمحاكاة - الدكتور علي الجازي

[Suzana]

النمذجة والمحاكاة للآلات الكهربائية
Electric Machines

الجزء الخامس
نمذجة آلات التيار المتناوب
المحرك التزامني




1) مقدمة
الآلات التزامنية هي تلك الآلات التي تدور بالسرعة التزامنية , وعلى الرغم من أن تصميم الآلات التزامنية ثلاثية الطور ذو تكلفة باهظة بمقرانته مع الآلات التحريضية إلا أن أدائها العالي عند الاستطاعات الكبيرة يغطي على تكلفتها العالية , حيث تستخدم الآلات التزامنية بشكل واسع في محطات التوليد الكبيرة وكذلك في نظم القيادة الضخمة.
وتمثل الآلة على المحورين المتعامدين (d,q) كما هو مبين بالشكل التالي....

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image001.png[/IMG]

2) النموذج الرياضي للآلة التزامنية ثلاثية الطور
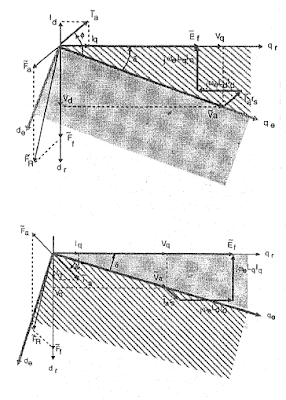
الأشكال التالية توضح الأنماط المختلفة لعمل الآلة التزامنية .....

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image002.png[/IMG]
العمل كمحرك بمعامل استطاعة متقدم(الشكل العلوي) ومتأخر(الشكل السفلي)

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image003.png[/IMG]
العمل لمولد بمعامل استطاعة متقدم (الشكل العلوي) ومتأخر (الشكل السفلي)

الانتقال من نموذج المحاور الثلاثية (abc) إلى المحورين المتعامدين (dq) يتم وفق المعادلات التالية :

أو يمكن إجراء التحويل بشكل آخر بخطوة واحدة وفق المعادلات التالية :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image010.png[/IMG]

وللتعبير عن معادلات الجهد على المحاور المتعامدة (dq) كتكامل للسيالة التسربية للملفات , فإن المعادلات السابقة والتي تصف جهد الثابت يمكن أن تحول لكي تحل معادلات السيالة التسربية للملفات. وفي حالة الآلة بملف حقل واحد فقط على المحور المباشر وزوج من ملفات الإخماد على المحورين المتعامدين , فإن معادلات السيالة على المحاور المتعامدة تصبح :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image032.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image033.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image034.png[/IMG]

حيث :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image035.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image036.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image037.png[/IMG]

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image038.png[/IMG]

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image039.png[/IMG]

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image040.png[/IMG]

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image041.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image042.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image043.png[/IMG]

لابد من ملاحظة أن المعادلات العلوية هي من أجل المحرك , والتي تكون التيارات فيها مع القطبية الموجبة للجهد المطبق على ملفات الثابت. وسنعبر عن السيالة التسربية المتشابكة كتابع للسيالة الكلية التسربية في الملفات بحيث تكون المعادلات :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image044.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image045.png[/IMG]

حيث :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image046.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image047.png[/IMG]

وبعد الحصول على قيم السيالة التسربية للملفات والسيالة التشابكية التسربية على المحورين المتعامدين يمكن تحديد تيارات الملفات حسب المعادلات التالية :

[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image050.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image051.png[/IMG]
[IMG]file:///C:\Users\ENG~1.ADN\AppData\Local\Temp\msohtmlclip1 \01\clip_image052.png[/IMG]

التيارات على المحاور المتعامدة يمكن الحصول على القيم المكافئة لها على نموذج المحاور الثلاثية وفق المعادلات التالية :

التعبير بالقيم الواحدية لمعادلة العزم ومعادلة حركة الدائر :
عند دراسة نظم القدرة حيث يكون هناك العديد من المحولات وكذلك تجهيزات متعددة في الشبكة فلابد من أخذ نقطة أساس للعمل والعمل بالقيم الواحدية عندها (النسب للأساس).
دراستنا تتضمن فقط ألة تزامنية واحدة ولذلك لن نستفيد من جميع نواحي استخدام النسب.

3) نموذج المحاكاة








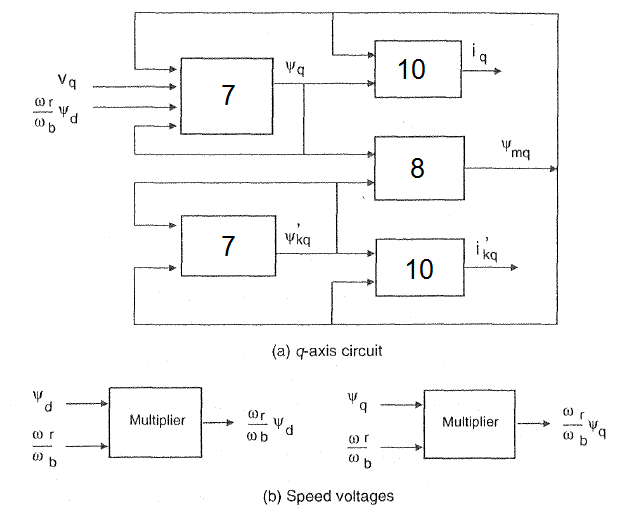
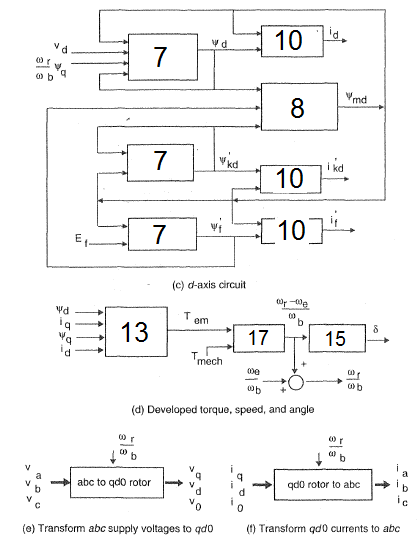
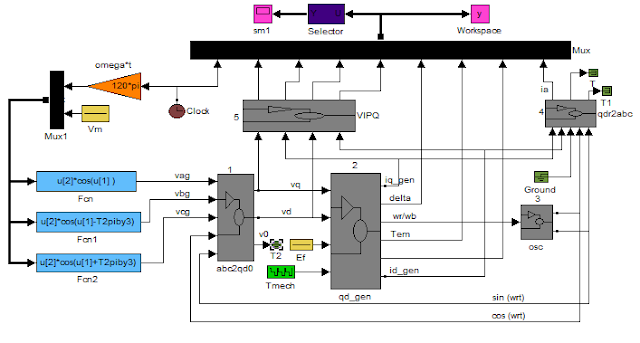
...1...



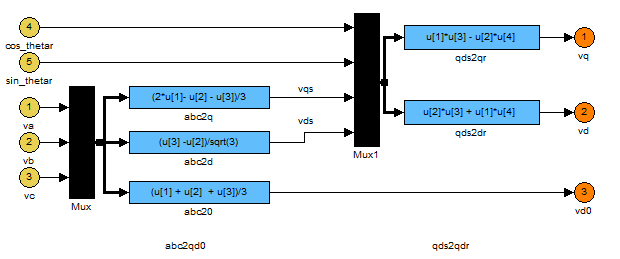
...2...

...q_cct...

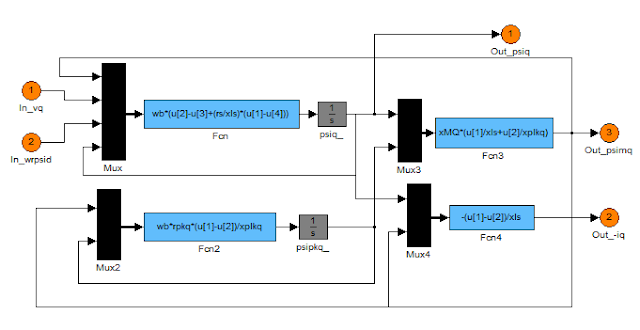
...d_cct...



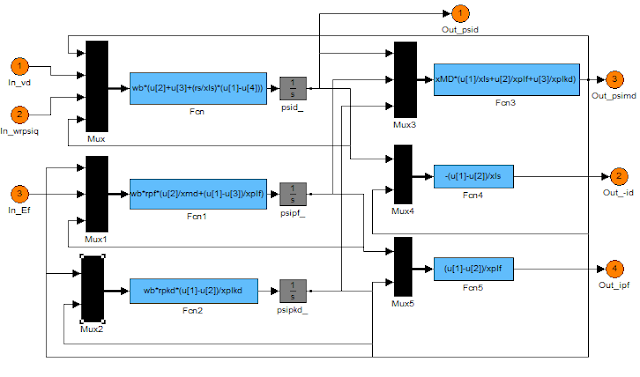
...Rotor...



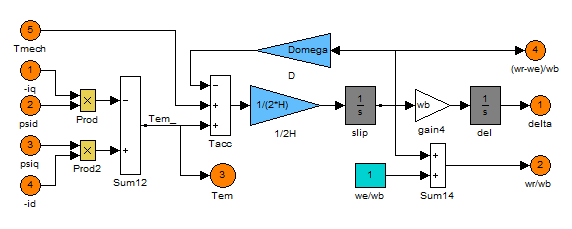
...3...

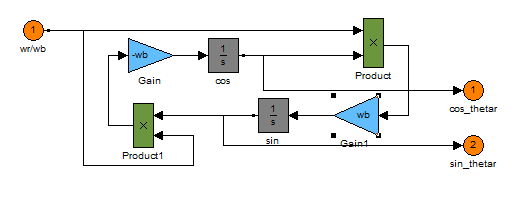
...4...




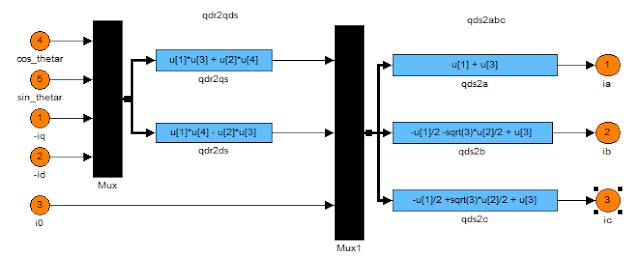
...5...

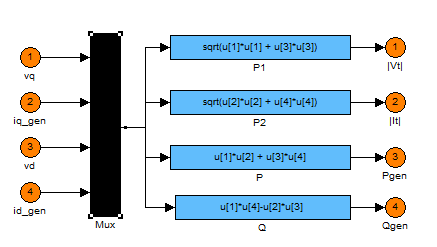
المصدر :

Dynamic Simulation of Electric Machinery Using MATLAB/Simulink

---------------------------------------------------------------------------------------------------------------------------------------------

نمذجة ومحاكاة إلكترونيات القدرة الكهربائية
Power Electronics
الجزء الأول



:مقدمة
إن دراسة دارات أنصاف النواقل (ديود - ثيرستور) ترتبط بعلم الإلكترونيات وبسبب تقنية تصنيع هذه العناصر والدوائر الثانوية اللازمة للقيادة وللإقلاع ونظراً لانتشار التطبيقات العملية لعلم الثيرستور واستخدامه في أغلب أنظمة القيادة والتحكم الآلي فرأيت أنه لابد من البحث في هذه التطبيقات والعمل على استخدام برنامج الماتلاب في نمذجة ومحاكاة دارات القيادة المختلفة.
سنناقش بإذن الله في الدروس القادمة المواضيع التالية :
1 - دارات التقويم (أحادية وثلاثية الطور) AC\DC Converter
2 - قيادة محرك التيار المستمر في الأرباع الأربعة DC Drive
3 - دارات التعريج (أحادية وثلاثية الطور) DC\AC Inverter
4 - مبدلات التردد CycloConverter
5 - DC\DC and AC\AC
6 - مواضيع متممة (PWM - SVPWM - FOC - Vector control)
سنعتمد على مكتبة SimpowerSystems في نمذجة داراتنا في الماتلاب


أولاً : العناصر أنصاف النواقل المستخدمة في إلكترونيات القدرة

• الثنائي نصف الناقل - الديود

الشكل المبين يبين منحني خواص التشغيل للديود

• الثيرستور (مقوم سلكوني مقاد) عنصر نصف ناقل من مادة سيليكونية , ذي طبقات أربع متناوبة PNPN مزود بإلكترود للتحكم (Gate)

• ترانزستور الاستطاعة IGBT

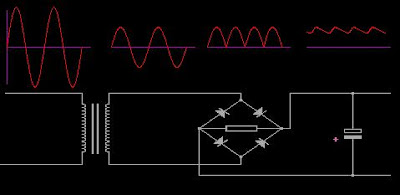
ثانياً : دارات التقويم AC\DC Converter

• دارات التقويم أحادية الطور

سنناقش نموذجين مختلفين لدارات تقويم موجة كاملة , إن مقوم الموجة الكاملة يحول قدرة الدخل إلى الخرج خلال نصفي موجة الدخل كليهما ويقدم تياراً متوسطاً أكبر لكل دور مقارنة مع مقوم نصف الموجة. يجب استخدام محولة مع هذا المقوم للحصول على القطبيات الموجبة والسالبة للموجة.
والشكل التالي يبين الدارة المطلوبة لذلك :


النموذج الأول :



نموذج الماتلاب المقابل لهذه الدارة :





نجعل بارامترات كافة عناصر الدارة على قيمها الإفتراضية ونقوم فقط بالتعديل على المنبع والحمل وذلك كما هو مبين بالأشكال التالية ...















بعد ذلك ومن أجل تشغيل سليم لنموذج المحاكاة نقوم بكتابة برنامج بسيط يطلب من المستخدم إدخال قيم الحمل (تحديد طبيعة الحمل) وذلك كما بالشكل التالي
Matlab Script

بعد إدخال قيمة الحمل وتشغيل النموذج يمكن مشاهدة الأشكال بكتابة السطر التالي في نافذة الماتلاب الرئيسية (Command window) :



النتائج التالية من أجل حمل أومي بمقاومة 90 أوم ....


التيار

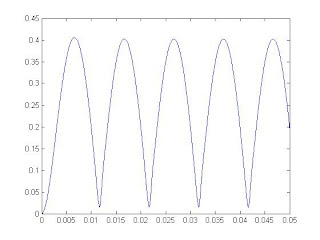
التوتر

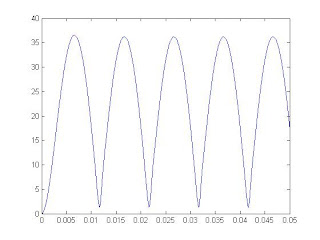
النموذج الثاني :
يمكن تحقيق موجة كاملة دون اللجوء إلى استخدام محولة وكمثال على ذلك المقوم الجسري المبين

لتحليل هذه الدارة نقول عندما يكون جهد الدخل (المنبع) موجباً , يوصل الثنائيات العلوي اليميني والسفلي اليساري ويكون الثنائيان الثانيان كدارة مفتوحة , وعندما يصبح المنبع سالب يصبح العكس .....


نموذج الماتلاب المقابل لهذه الدارة :



التعديلات في هذا النموذج مشابهة تماماً للنموذج السابق .....
كذلك نقوم ببرنامج بسيط مشابه للسابق لكي يحدد المستخدم قيمة الحمل


النتائج :

• دارات التقويم ثلاثية الطور

أولاً : مجموعة التقويم التفرعية البسيطة
سنناقش مجموعة التقويم البسيطة المقادة (بزوايا قدح مختلفة) وغير المقادة ....


المخطط التالي يبين نموذج المحاكاة لمجموعة تفرعية بسيطة غير مقادة مع النتائج



والمخطط التالي يبين نموذج المحاكاة لمجموعة تفرعية بسيطة مقادة من أجل احمال مختلفة وزوايا قدح مختلفة ....





ثانياً : مجموعة التقويم التفرعية المضاعفة



شرح عناصر النموذج :

1 - مولد نبضات متزامن (من أجل جسر كريتز)



2 - Thyristor Converter جسر تقويم كريتز (موجود في مكتبة الماتلاب باسم Universal Bridge)



3 - Selecter : مهمة هذا العنصر الفصل بين النبضات التي تدخل إليه وعددها (6) , نستعين به من أجل رؤية النبضات المتزامنة والخارجة من مولد النبضات المتزامن



النتائج :
حمل مختلط زاوية قدح 30





حمل تحريضي زاوية قدح 90




تسلسل النبضات عند زاوية 30





كافة التوترات





المصدر :
1 - إلكترونيات القدرة الكهربائية 1 - الدكتور هاشم ورقوزق - منشورات جامعة دمشق
Power Electronics 1 - Dr. Eng. Hashem OIRKOZEK
2 - أسس الهندسة الإلكترونية - الدكتور عبد الرزاق البدوية , الدكتور نديم شاهين
Fundamentals of Electronic Engineering
3 - MATLAB / help
4 - www.mathworks.com
5 - http://en.wikipedia.org

المصدر
http://matlab4engineering.blogspot.c...-machines.html

[YHNM]

شكرا سوزانا وعاشت يديك
تقييمي المتواضع

[عماد الحمزاوي]

[Asinat]

مجهود قيم سوزانا ...تقييم مستحق

[Suzana]

بالخدمة شكرا للمرور والتعليق وقبلها الشكر لصاحب الموضوع