01 من 05
الأرقام البابلية
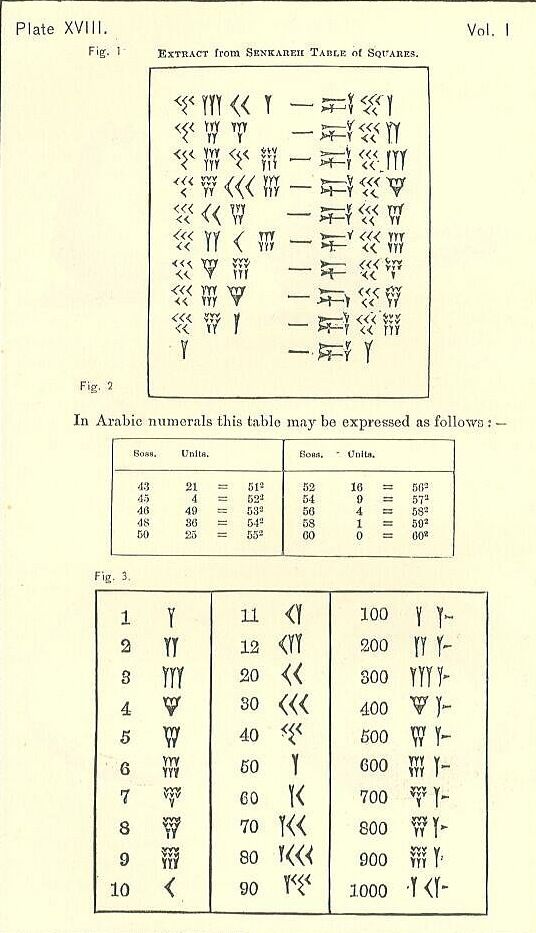
Senkareh Table of Squares (Plate 18). هنا مثال على الرياضيات البابلية ، مكتوبة بالكتابة المسمارية. مع هذا الجدول من المربعات ، يمكنك أن ترى كيفية وضع Base 60 موضع التنفيذ.
- السبع ممالك العظمى ، جي. رولينسون
ثلاث مناطق رئيسية من الفرق من أرقامنا
عدد الرموز المستخدمة في الرياضيات البابلية
تخيل مدى سهولة تعلم الحساب في السنوات الأولى إذا كان كل ما عليك فعله هو تعلم كيفية كتابة خط مثل أنا والمثلث. هذا في الأساس كان على كل الناس القدماء في بلاد ما بين النهرين أن يفعلوا ، على الرغم من أنهم كانوا يتنوعون بينهم هنا ، هناك ، مطول ، تحول ، إلخ.
لم يكن لديهم أقلامنا وأقلام الرصاص ، أو الورق لهذه المسألة. ما كتبوه كان أداة يستخدمها المرء في النحت ، حيث أن الوسيلة كانت طينية. سواء كان ذلك أصعب أو أسهل في تعلم كيفية التعامل معه من قلم الرصاص ، فإن الأمر لا يزال قادمًا في قسم السهولة ، مع وجود رمزين أساسيين فقط للتعلم.
القاعدة 60
الخطوة التالية يلقي مفتاح في قسم البساطة. نستخدم قاعدة 10 ، وهو مفهوم يبدو واضحًا لأن لدينا 10 أرقام. لدينا بالفعل 20 ، ولكن دعونا نفترض أننا نرتدي الصنادل بأغطية واقية لحماية القدم من الرمال في الصحراء ، حار من الشمس نفسها التي من شأنها أن تخبز أقراص الطين والحفاظ عليها بالنسبة لنا للعثور على آلاف السنين في وقت لاحق. استخدم البابليون هذه القاعدة 10 ، ولكن في جزء منها فقط. استخدموا في الأساس Base 60 ، وهو نفس العدد الذي نراه حولنا في دقائق ، وثواني ، ودرجات مثلث أو دائرة. لقد أنجزوا علماء فلك ، وهكذا كان العدد قد جاء من ملاحظاتهم على السماء. يحتوي Base 60 أيضًا على العديد من العوامل المفيدة التي تجعل من السهل حسابها. ومع ذلك ، فإن الاضطرار إلى تعلم القاعدة 60 أمر مرعب.
في "تكريم لبابل" [ الجريدة الرياضية ، المجلد. 76 ، رقم 475 ، "استخدام تاريخ الرياضيات في تدريس الرياضيات" (Mar.، 1992) ، ص. 158-178] ، الكاتب-المعلم نيك ماكينون يقول إنه يستخدم الرياضيات البابلية لتدريس 13 عامًا شيخوخة حول قواعد غير 10. يستخدم النظام البابلي قاعدة -60 ، بمعنى أنه بدلاً من أن يكون عشريًا ، فإنه جنسياً.
النتيجة الآن 1: 1 في قسم البساطة.
التدوين الموضعي
يعتمد كل من نظام الرقم البابلي و نظامنا على الموقع لإعطاء قيمة. يقوم النظامان بشكل مختلف ، جزئياً لأن نظامهما يفتقر إلى الصفر. إن تعلم النظام البابلي اليساري إلى اليمين (الأعلى إلى المنخفض) من أجل المذاق الأول للحساب الأساسي ربما لا يكون أكثر صعوبة من تعلم نظامنا الثنائي الاتجاه ، حيث يتعين علينا أن نتذكر ترتيب الأرقام العشرية - زيادة من الرقم العشري وأولئك العشرات والمئات ، ثم ينتشرون في الاتجاه الآخر على الجانب الآخر ، لا يوجد عمود واحد ، أو أعشار ، أو مائة ، أو ألف ، إلخ.
التعادل لا يزال.
سوف أذهب إلى مواقف النظام البابلي في صفحات أخرى ، ولكن هناك بعض الكلمات المهمة التي يجب تعلمها أولاً.
السنوات البابلية
نتحدث عن فترات من السنوات باستخدام الكسور العشرية. لدينا عقد لمدة 10 سنوات ، قرن لمدة 100 سنة (10 عقود) أو 10X10 = 10 سنوات مربعة ، و ألفية لمدة 1000 سنة (10 قرون) أو 10X100 = 10 سنوات مكعبة. لا أعرف أي مصطلح أعلى من ذلك ، لكن هذه ليست الوحدات التي استخدمها البابليون. يشير نيك ماكينون إلى قرص من Senkareh (لارسا) من السير هنري رولينسون (1810-1895) * للوحدات التي استخدمها البابليين وليس فقط للسنوات المعنية ولكن أيضًا الكميات التي تنطوي عليها:
- سوس
- نير
- سار .
الطحلب يشير إلى فترة 60 عاما. إن ner هي وحدة من 600 سنة ، أو مرة واحدة soss 10 [في حين يوصف النظام البابلي على أنه جنس ، هو أيضا عشري جزئي] و sar ، وحدة من 3600 سنة - a soss squared.
لا يوجد رابط التعادل: ليس بالضرورة أن يكون من الأسهل تعلم مربعات السنة المربعة والمشتقة من اللاتينية أكثر من مقاطع البابلية التي لا تتضمن مكعبات ، ولكن الضرب في 10.
ما رأيك؟ هل كان من الصعب تعلم أساسيات العدد كطفل في مدرسة بابلية أو كطالب حديث في مدرسة ناطقة باللغة الإنجليزية؟
* جورج رولينسون (1812-1902) ، شقيق هنري ، يعرض جدولاً مبسّطًا من المربعات في الممالك السبع الكبرى للعالم الشرقي القديم . يبدو الجدول فلكيًا ، استنادًا إلى فئات السنوات البابلية.
تأتي جميع الصور من هذه النسخة الممسوحة ضوئياً عبر الإنترنت من طبعة تعود إلى القرن التاسع عشر من عهدالملك جورج رولينسون "الممالك السبع الكبرى للعالم الشرقي القديم" .
02 من 05
أعداد الرياضيات البابلية
الجدول المسماري من المربعات
- السبع ممالك العظمى ، جي. رولينسون
منذ نشأتنا مع نظام مختلف ، فإن الأرقام البابلية مربكة.
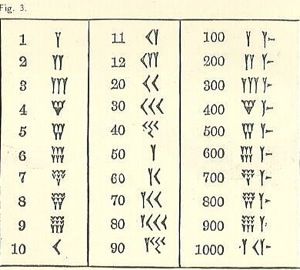
على الأقل ، يتم تشغيل الأرقام من أعلى اليسار إلى منخفض على اليمين ، مثل نظامنا العربي ، لكن البقية ربما تبدو غير مألوفة. الرمز الخاص بواحد هو شكل إسفين أو شكل حرف Y. لسوء الحظ ، يمثل Y كذلك 50. هناك بعض الرموز المنفصلة (جميعها تستند إلى الوتد والخط) ، ولكن يتم تكوين جميع الأرقام الأخرى منها.
تذكر أن شكل الكتابة مسمارية أو إسفينية الشكل. بسبب الأداة المستخدمة لرسم الخطوط ، هناك مجموعة محدودة. قد يكون الإسفين أو لا يكون له ذيل ، مرسومة بسحب قلم الكتابة المسمارية على طول الطين بعد أن يطبع شكل مثلث الجزء.
يبدو الرقم 10 ، الذي تم وصفه على أنه رأس سهم ، مثل <تمدده إلى حد ما.
تظهر ثلاثة صفوف تصل إلى 3 1s صغيرة (مكتوبة مثل Ys مع بعض ذيول مختصرة) أو 10s (10 مكتوبة مثل <) تتجمع معاً. يتم ملء الصف العلوي أولاً ، ثم الثاني ، ثم الثالث. انظر الصفحة التالية.
03 من 05
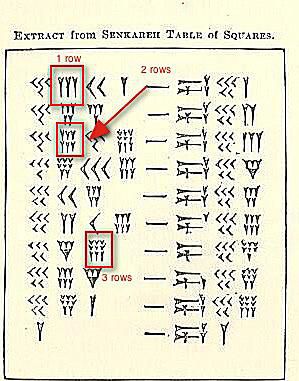
صف واحد و 2 صفوف و 3 صفوف
جدول المربعات.
- السبع ممالك العظمى ، جي. رولينسون
توجد ثلاث مجموعات من مجموعات الأرقام المسمارية موضحة في الرسم التوضيحي أعلاه.
في الوقت الحالي ، لا نشعر بالقلق لقيمتها ، ولكن مع توضيح كيف سترى (أو تكتب) في أي مكان من 4 إلى 9 من نفس العدد مجمعة معًا. ثلاثة تذهب في صف واحد. إذا كان هناك رابع أو خامس أو سادس ، فإنه يذهب أدناه. إذا كان هناك السابعة أو الثامنة أو التاسعة ، فأنت بحاجة إلى صف ثالث.
تستمر الصفحات التالية مع تعليمات حول إجراء العمليات الحسابية مع المسمارية البابلية.
04 من 05
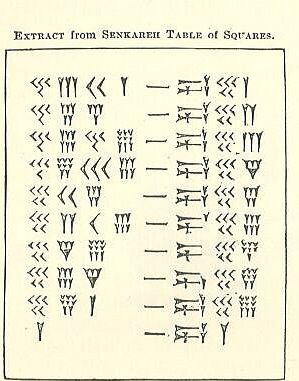
جدول المربعات
Senkareh، جدول، بسبب، المربعات، إلى داخل،
- السبع ممالك العظمى ، جي. رولينسون
من ما قرأته أعلاه حول السوس - الذي ستتذكره هو البابلي لمدة 60 عامًا والاسفين ورأس السهم - وهي أسماء وصفية لعلامات مسمارية ، انظر ما إذا كان بإمكانك معرفة كيفية عمل هذه الحسابات. جانب واحد من علامة شبيهة بالشرطة هو الرقم والآخر هو المربع. جربها كمجموعة. إذا لم تستطع معرفة ذلك ، فابحث عن الخطوة التالية.
05 من 05
كيفية فك شفرة المربعات
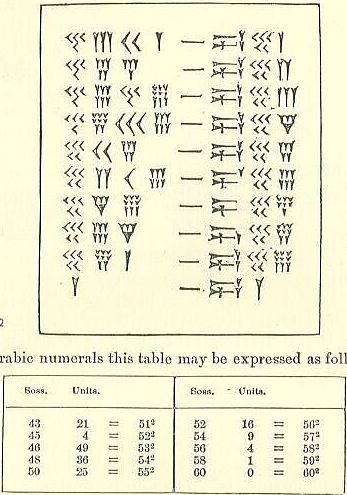
التحويل العربي للجدول المسماري للمربعات.
- السبع ممالك العظمى ، جي. رولينسون
يمكنك معرفة ذلك الآن؟ اعطها فرصة.
...
هناك 4 أعمدة واضحة على الجانب الأيسر متبوعة بعلامة شبيهة بالشرطة و 3 أعمدة على اليمين. وبالنظر إلى الجانب الأيسر ، فإن ما يعادل عمود 1s هو في الواقع أقرب عمودين إلى "الشرطة" (الأعمدة الداخلية). يتم حساب الأعمدة الخارجية الأخرى 2 كعمود 60 ثانية.
الرمز في أعلى اليسار هو لـ 4 (3-
- 4 - أقل من 40
- 3-Ys = 3.
- 40 + 3 = 43.
- المشكلة الوحيدة هنا هي أن هناك رقم آخر بعدها. هذا يعني أنها ليست وحدات (مكان "هؤلاء"). 43 ليست 43 ، ولكن 43-60 ، لأنه نظام sexagesimal (الأساس -60) وهو في عمود الطحين كما يشير إلى الجدول السفلي.
- اضرب 43 في 60 للحصول على 2580.
- أضف العدد التالي (2-
- لديك الآن 2601.
- هذا هو مربع 51.
يحتوي الصف التالي على 45 في عمود soss ، لذا قمت بضرب 45 × 60 (أو 2700) ، ثم أضف 4 من عمود الوحدات ، بحيث يكون لديك 2704. الجذر التربيعي لـ 2704 هو 52.
يمكنك معرفة لماذا العدد الأخير = 3600 (60 مربع)؟ تلميح: لماذا لم يكن 3000؟





 رد مع اقتباس
رد مع اقتباس