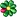كانت الطريقة التي اوجدها كانتور لجعل المجموعات العددية اللا متناهية قابلة للعد فعّالة عندما يتعلق الامر بالاعداد النسبية, ولكننا توقفنا في الجزء السابق عند التساؤل فيما اذا كان نفس الامر ينطبق على الاعداد غير النسبية.
فنحن نعلم أنه لا يمكن كتابة الأرقام غير النسبية على هيئة كسور, وانما فقط كأعداد عشرية حيث تستمر تلك الاعداد إلى أجل غير مسمى. أثبت كانتور أنه عندما يكون لدينا سلسلة من هذه الأعداد العشرية اللانهائية ، فمن الممكن دائما إنشاء العديد من المجموعات داخل تلك السلسلة, و في كل مجموعة سيكون هناك عدد لا نهائي من العناصر.
هذا يعني أنه عندما نوسع كمية الأرقام لتشمل الأعداد غير النسبية, اضافة الى الاعداد الحقيقية, نحصل على شكل مختلف من اللانهاية للاعداد النسبية. انها الان غير قابلة للعدد وهي اكبر او اقوى كما يقول كانتور.
يتوافق مصطلح "غير قابل للعد" من نواحٍ عديدة مع اللانهاية التي نفكر فيها عندما نقسم خطا مرات لا تحصى, أو عندما نفكر في المسافة التي سيجريها أخيل في مفارقة زينون القديمة للوصول إلى السلحفاة.
أصبحت المسافة أقصر وأقصر ، لكن وفقا لزينون ،لا تصبح ابدا صفرا. لم يوافق كانتور على ادعاء زينون, وكانت حجته على النحو التالي:
كسر عشري لانهائي يتقارب نحو - أي يقترب - من عدد صحيح ، على سبيل المثال 0 ، له نفس خصائص العدد نفسه وبالتالي فهو مساوي له. على سبيل المثال ، يمكننا التفكير في العدد العشري 0.1 ونقسمه على 10 لمرات ومرات. ثم نحصل على 0.01 أولا ، ثم 0.001 ، ثم 0.0001 وهكذا. إذا تخيلنا أن هذا يحدث مرات عديدة بشكل لا نهائي ، إذن لدينا رقم يمكن كتابته على النحو التالي:( 0.00… 1 )- حيث تمثل النقاط الثلاث عددا لا نهائيا من الأصفار.
بمعنى آخر لن نصل أبدا إلى الرقم 1 ، وبالتالي فإن الرقم عمليا هو صفر ضخم جدا.
وبالتالي ، فإن المسافة بين أخيل والسلحفاة ستصبح في بعض الأحيان صفرا ، وان اخيل سيلحق بالسلحفاة في مرحلة ما... بل وسيتجاوزها.
لم تنل أفكار وأدلة جورج كانتور تلك قبولا لدى الجميع . كان عالم الرياضيات الفرنسي هنري بوانكاريه من أشد المعارضين لاراء كانتور وقد صرح بازدراء:
"ستنظر الأجيال القادمة إلى نظرية المجموعات على أنها مرض عانوا منه".
حتى استاذ كانتور السابق في جامعة برلين ، ليوبولد كرونكر ، لم يكن لديه أي شيء لطيف ليقوله عن نتائج كانتور:
"لا أعرف ما الذي يهيمن على نظرية كانتور , سواء كانت فلسفة أم لاهوتا , لكنني متأكد من أنها لا علاقة لها بالرياضيات".
على ما يبدو ، من وجهة نظر مهنية ، اختلف كرونكر تماما مع تلميذه السابق ، لكن كلماته القاسية تشير بوضوح إلى جانب مختلف تماما من كانتور ... معتقداته.
كان كانتور متدينا جدا ، وبالتالي كان من المهم أيضا بالنسبة له أن يتوافق عمله الرياضي مع مفهومه عن الله.
بالنسبة إلى كانتور ، لم تكن اللانهاية مجرد احتمالات ممكنة ، كما ادعى أرسطو. لقد كانت اللانهاية حقيقة مثل أي شيء آخر في الرياضيات وبالتالي مثل كل شيء آخر في العالم. مثل غاليلو، لم ير كانتور الرياضيات على أنها شيء ابتكره الإنسان بشكل تجريدي ، ولكن كشيء أساسي خلقه الله ووضعه في الطبيعة. وما خلقه الله لديه أيضا القدرة على تحقيقه. يقول كانتور:
"الخوف من اللانهاية هو شكل من أشكال رؤية النفق الذي يحطم إمكانية رؤية اللانهائي الحقيقي ، على الرغم من أنه في أعلى صوره قد خلقنا وغذانا ، وفي أشكاله الثانوية اللانهائية يحيط بنا في كل مكان وهو موجود دائما في اذهاننا "... يعني باللا متناهي الحقيقي:
الله
استمرت المعركة بين كرونكر وكانتور خلال عقدين من الزمن حتى وفاة كرونيكر في عام 1891. وكان كل منهما يمثل اتجاه مختلف عن الاخر في الرياضيات ، والتي قسمت علماء الرياضيات في ذلك الوقت إلى معسكرين. فبالنسبة إلى كانتور ، كانت الرياضيات و الأرقام ـ بما في ذلك الاعداد غير النسبية ـ حقيقة واقعية . اما بالنسبة إلى كرونكر ، كان العدد حقيقيا فقط عندما يمكن للمرء أن يرى وجوده المادي ، مما يعني أيضًا أنه يستمتع بالاعداد النسبية دون سواها.
أدى عدم الاعتراف من معلمه القديم إلى خسائر فادحة لكانتور وربما ساهم في الكساد الذي عانى منه في وقت لاحق من حياته. واصل كانتور عمله في الرياضيات ، ولكن في نهاية مسيرته المهنية في جامعة هالي قللها تدريجيا وركز على اهتماماته الأخرى: الفلسفة والأدب.
ومع ذلك فتح المزيد والمزيد من الناس أعينهم تدريجيا على جودة عمل كانتور الرياضي وايجاده لنظرية المجموعات. كان ديفيد هيلبرت من أعظم المعجبين بكانتور ، وقد وصف نتائجه بأنها :
"أفضل نتاج للعبقرية الرياضية وأحد أفضل إنجازات النشاط البشري الفكري البحت".
في وقت لاحق ابتكر هيلبرت تصورا شهيرا للا نهائيات كانتور القابلة للحساب ,سُمي بـ :
"فندق هيلبرت".
الفكرة هي أن نتخيل فندقا افتراضيا به عدد نهائي من الغرف ، مرقمة 1 ، 2 ، 3 ، 4 ، 5 وهكذا. وكل غرفة يسكنها نزيل, فلا توجد اي غرفة شاغرة. في احد الايام يصل ضيف جديد في وقت متأخر من المساء ، وبدلا من إرساله الى فندق اخر ، يختار موظف الاستقبال حل المشكلة. يطلب من الضيف في الغرفة 1 الانتقال إلى الغرفة 2 والنزيل في الغرفة 2 الانتقال إلى الغرفة 3 والنزيل في الغرفة 3 الانتقال إلى الغرفة 4 ... وهكذا. وبهذه الطريقة نحصل على غرفة شاغرة ، وهي الغرفة 1 ، التي ينتقل إليها الضيف الجديد. وبحسب الرياضيات المجردة فان هذا المثال تعبر عنه المعادلة التالية: ∞ + 1 = ∞.
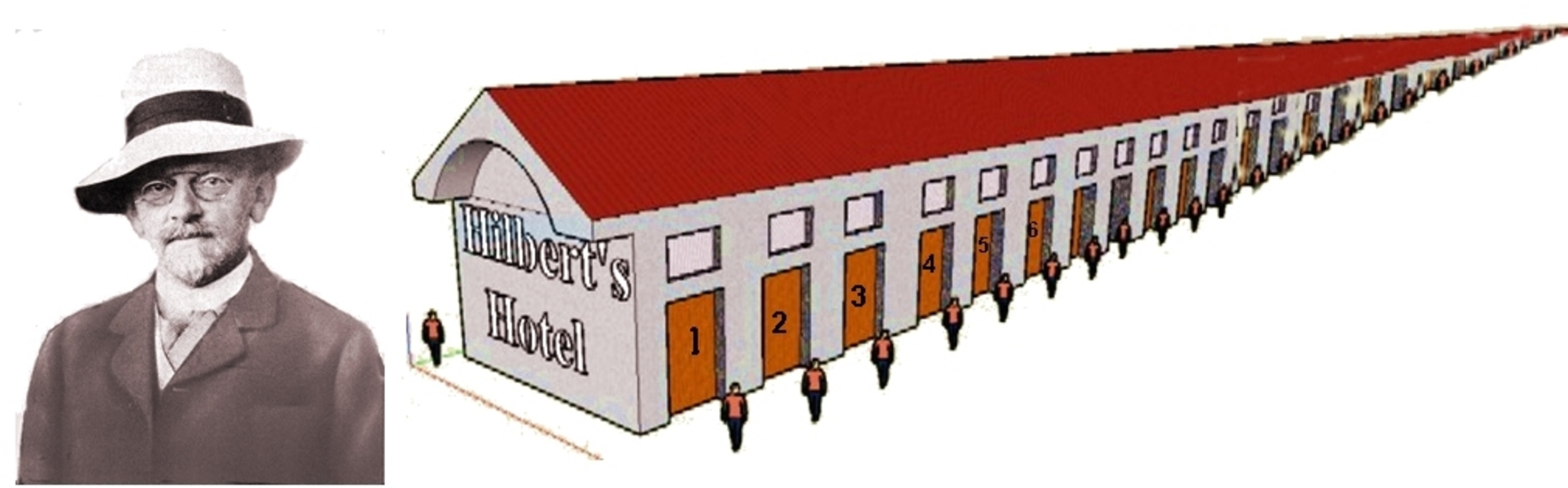
في هذه الليلة لا احد من نزلاء فندق هيلبرت سيتمكن من النوم ، لأنه بعد وقت قصير ستصل حافلة بعدد لا حصر له من الضيوف. وايضا هذه المرة عبقرية موظف الاستقبال ستعالج الموقف. اذ يوقظ الموظف جميع النزلاء مرة أخرى ويطلب منهم الآن مغادرة غرفهم ثم الانتقال إلى أقرب غرفة شاغرة برقم زوجي.
أولا ينتقل الضيف من الغرفة 1 إلى الغرفة 2 ، ثم ينتقل الضيف من 2 إلى 4 ، والضيف التالي من 3 إلى 6 ... وهكذا. ثم يمكن للوافدين الجديد الانتقال إلى الغرف ذات الارقام الفردية.
ومع ذلك ، لا يزال على ضيوفنا الصبورين البقاء مستيقضين. لأنه فجأة يصل ما لا يقل عن عدد لا حصر له من الحافلات ، وكلها تحتوي على عدد لا حصر له من الركاب. هنا يجب أن يفكر موظف الاستقبال قليلا قبل أن يجد الحل.
أولا ، يطلب من جميع ضيوفه مغادرة غرفهم والانتقال إلى غرف ذات أرقام فردية 1 و 3 و 5 و 7 و 9 ...الخ. إنهم ييقنطون الآن في غرف يمكن كتابتها رياضيا ( 2n - 1) ، حيث n هي أرقام الغرف. تحصل المجوعة التالية على الغرف التي يمكن كتابتها ( 2 *(2n - 1)). المجموعة الثالثة تحصل على الغرف بأرقام مضاعفة للمجموعة السابقة ، أي ( 4 *(2n - 1)). بهذه الطريقة استطاع موظف الاستقبال ان يوزع المجموعات التالية من الضيوف اللامحدود ... بلا حدود. فهناك دائما توجد مساحة كافية.
بمثاله أظهر ديفيد هيلبرت نقطة مهمة في نظرية كانتور للمجموعات ، واستخدمها على نطاق واسع في محاضراته. اذ يُظهر فندق هيلبرت أن :
∞ + ∞ = ∞ وأن ∞ x ∞ = ∞.
أي ان ناتج جمع او ضرب مجموعتين لا متناهيتين يساوي دائما مجموعة لا متناهية.
والان كونوا صبورين كنزلاء فندق هيلبرت وابقوا معنا ..حتى الجزء القادم
حصري لمنتديات درر العراق
الجزء السابق





 رد مع اقتباس
رد مع اقتباس