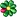أفعى مراوغة تنساب متعرجة في الرياضيات, وبين الحين والاخر تبرز رأسها في الفيزياء لتنشأ مفارقات تجعلنا نعيد النظر فيما توصلنا اليه, انها :
اللا نهاية!
لم يمض اكثر من مئة عام عندما توصل علماء الرياضيات الى حساب الكميات اللا نهائية, ولكن يبقى السؤال الأهم:
هل وجود اللا نهاية مقتصر فقط على العالم الخيالي للارقام؟ أم انه جزء من الواقع؟
قبل 100 عام وضعت نوبة قلبية حدا لأحد أعظم العباقرة الرياضيين في تاريخ العالم. ودع جورج كانتور الحياة يوم 6 يناير 1918 وحده في غرفته في مصحة للأمراض النفسية في هالي بألمانيا. في ظل الحرب العالمية الأولى قضى أيامه الأخيرة في حالة فقر ، أضعفه الجوع وعذبه الاكتئاب الذي طارده لعقود.
و من المشكوك فيه ما إذا كان جورج كانتور قد رأى نفسه كواحد من العظماء في مجاله. فقد تميز معظم حياته المهنية بالنقد والمعارضة من علماء الرياضيات الآخرين ، الى درجة جعلته يشك بنفسه مرات عدة. بالنسبة إلى علماء الرياضيات المعاصرين بدت لهم نظرياته أيضا مثل الجنون النقي. فمما ادعاه أنه لا يوجد شكل واحد فقط بل شكلين من اللانهاية.
يتفق علماء الرياضيات اليوم ، مع ذلك ، على أن مساهمته في الرياضيات كانت لا تقدر بثمن لأنه أعطانا فهما جديدا تماما لمفهوم اللانهاية.
لنفهم إنجازات كانتور ، يجب أن نعود إلى الوراء لآلاف السنين .ربما كانت فكرة اللانهاية قد سحرت وعذبت الإنسان منذ أن بدأ أسلافنا ينظرون إلى السماء ويفكرون في مدى بعدنا عن النجوم ، وما الذي يكمن وراءها. فكرة اللانهاية مذهلة ، والمفارقة هي أننا خائفون منها بينما لا يمكننا الاستغناء عنها. الادعاء بأن الكون لانهائي غالبا ما يعطي رد فعل: "يجب أن ينتهي في مكان ما". وعلى العكس نواجه صعوبة في تقبل فكرة الكون المحدود ، لأنه سيواجهنا التساؤل التالي: "ما الذي خارج الكون إذن؟".
لم تتضاءل المفارقة منذ ظهور الأداة الأساسية للعلوم: الرياضيات.
هنا تظهر اللانهائية في كل مكان ، ولكن هل يعني ذلك أيضا أنها جزء من الفيزياء؟ ربما يجيب معظم الفيزيائيين بالنفي. فانهم عندما يطورون نظريات تصف الواقع وتدخل اللا نهاية في معادلاتهم ، فإنهم عادة ما يرونها إشارة على أنه يجب أن يكون هناك خطأ ما في النظرية.
من ناحية أخرى ، أثبتت الرياضيات أنها أداة لا غنى عنها على الإطلاق لوصف الطبيعة ، فلماذا يكون هناك مثل هذا الاختلاف الكبير بين النظرية والواقع في الرياضيات والفيزياء؟
إن اللانهاية ليست مجرد رياضيات معقدة ومتقدمة. فليس على أي طفل ان يكون كبيرا في السن ليتعلم العد والحساب، وهو ليس ابعد من مسافة خطوة عن السؤال عن أكبر عدد. ألف أو مليون أو مليار أو ربما كوادريليون او قد يكون سكستليون ؟ فالانسان يتعلم بسرعة أن تسلسل الأرقام يستمر ، حتى بعد أكبر الأرقام المسماة على سبيل المثال جوجول ، وهو عبارة عن تسلسل واحد يليه مئة صفر. ومع ذلك ، لا يوجد رقم أكبر من اللانهاية.
في المدرسة نواجه (ما لا نهاية ) بالفعل عندما نبدأ في حساب الكسور والارقام العشرية. يمكن كتابة الكسر البسيط 1/3 على أنه 0.333333 ... ونعلم أن الرقم ثلاثة بعد الفاصلة يستمر إلى أجل غير مسمى. في الوقت نفسه في كتبنا الدراسية الأولى عن الهندسة نتعلم أن السطر يتكون من عدد لا نهائي من النقاط ، كل منها صغير الحجم بشكل لا نهائي.
بعد ذلك بقليل نتعلم أيضا كيف نشير الى اللا نهاية بعلامة خاصة ، ∞ ، والتي ربما ترمز إلى ثعبان يعض ذيله.
وعندما نغادر المدرسة تكون اللانهاية في عالم الرياضيات ظاهرة معروفة ومقبولة لنا جميعا.
في اليونان القديمة كانت اللقاءات الأولى مع اللانهاية أكثر دراماتيكية. ,كان فيثاغورس أحد عظماء الرياضيات وعاش من 570 إلى 495 قبل الميلاد أحد اولئك اليونايين الاوائل الذين تعاملوا مع اللا نهاية.
كان فيثاغورس متعدد المواهب الفنية وقد تعامل مع الفلسفة والرياضيات والموسيقى ،وقد اسس المدرسة الفيثاغورية وهي اخوية دينية تشكلت من طلابه واتباعه.
اليوم لا نعرف سوى القليل عن الرابطة الفيثاغورية اذ كان على المنتسبين لها, والذين يُطلق عليهم اسم (اخوة فيثاغورس ) أن يلتزموا السرية في انتمائهم لتلك المدرسة. ولكن في بعض المناطق كانوا متقدمين كثيرا عن وقتهم. على سبيل المثال ، دافعوا عن المساواة ، وبالتالي كانت النساء موضع ترحيب في الرابطة مثل الرجال.
من ناحية أخرى كان التفكير الحر محدودا عندما يتعلق الأمر باستجواب الحقائق الرياضية التي كانت سائدة في ذلك الوقت. على الأقل إذا أردنا أن نصدق قصة أحد طلاب فيثاغورس ، هيباسوس. خلال رحلة القارب عبر البحر الأبيض المتوسط أخبر هيباسوس أصدقائه في الأخوة عن بعض الأفكار التي كانت لديه حول ما نسميه اليوم نظرية فيثاغورس: أنه في مثلث قائم الزاوية توجد علاقة بين اضلاعه, بحيث ان مربع ( ضرب العدد بنفسه ) طول الوتر يساوي مجموع مربعي طولي الضلعين الآخرين.
قام هيباسوس بحساب المثلث البسيط الذي يكون طول كل ضلع منه 1 وبالتالي فان طول الوتر يساوي 2 √ , ثم توصل إلى استنتاج مفاده أن طول الوتر لا يمكن التعبير عنه بعدد صحيح ...ولا حتى بعدد كسري.
اثناء تلك الرحلة قام هيباسوس بتسلية زملائه المسافرين من خلال تقديم برهان رياضي على أنه لم يكن هناك عدد صحيح أو كسر مضروبا بنفسه ليصبح 2.
كان من الاجدر بهيباسوس ان لا يقوم بذلك ويفصح عما توصل اليه من نتائج. فقد شعر إخوانه بالذعر لدرجة أنهم ألقوا على الفور بهيباسوس في البحر وتركوه يلقى حتفه غرقا.
نحن اليوم نعلم أن هيباسوس كان على حق, وان 2 √ عدد غير نسبي. اليوم يمكننا كتابته كرقم عشري لنحصل على 1.414213562373095 ، إذا اخترنا الوقوف عند 15 رقما بعد الفاصلة. لكن الكسور العشرية مستمرة ولا يوجد نمط فيها كما هو الحال على سبيل المثال للكسر 1/3 ، حيث يمكننا التنبؤ بأن الرقم 3 سيستمر الى ما لا نهاية.
عدد اخر غير نسبي هو π او ما يعرف بثابت الدائرة, فلا يمكننا كتابته ككسر حتى اذا كان الكسر22/7 اقرب القيم له مع 15 رقما عشريا ، π = 3.141592653589793.
إن الأرقام غير النسبية التي كان هيباسوس على مسارها ستثبت نفسها لاحقا على أنها مهمة لنفهم بشكل اعمق مصطلح اللا نهائي ، ولكن قبل ذلك كانت هناك سلسلة طويلة من المخاوف التي كانت بانتظار أجيال من علماء الرياضيات والفلاسفة.
بعض أفضل الأمثلة هي المفارقات التي صاغها زينون الايلي، الذي عاش 490-425 قبل الميلاد. فقد حكى , على سبيل المثال ، قصة آخيل أو آخيليس الذي كان يركض ليلحق بالسلحفاة. كان لاخيل ان يجري عشرات المرات اسرع من السلحفاة، وذلك ما جعل زينون يعطي السلحفاة افضلية البدء في السباق مع اخيل, ولنقل ان المسافة بينهما كانت مئة متر. يمكننا ان نقول ان اخيل ـ بناءا على مفارقة زينون ـ لن يلحق بالسلحفاة أبدا. لأنه في اللحظة التي وصل فيها اخيل إلى المكان الذي كانت فيه السلحفاة في بداية السباق ، كانت السلحفاة قد وصلت إلى مسافة عشرة أمتار أخرى. وعندما وصل أخيل إلى ذلك المكان ، لكانت السلحفاة قد قطعت مترا اخرا... وهكذا ستنخفض المسافة بينهما باستمرار ، لكنها لن تكون صفرا أبدا.
لاحقا لفتت مفارقات زينون انتباه الفيلسوف الاغريقي أرسطو ، الذي عاش بين 384 و 322 قبل الميلاد, والذي كان مهتما جدا بمفهوم اللانهاية وتناولها في عمله "الفيزياء".
يدحض أرسطو مفارقات زينون ولكن بشكل غير مباشر .فبدلا من ذلك يميز ارسطو بين ما يسميه "اللانهاية المحتملة" و "اللانهاية الحقيقية". وهذا يعكس أيضا خلفية أرسطو الخاصة. بصفته ابن طبيب كان لديه نظرة ملموسة وعلمية للطبيعة ، وكطالب للفيلسوف أفلاطون كان لديه أيضا طريقة مجردة للنظر إلى العالم.
يدعي أرسطو بشكل أساسي أن اللانهاية موجودة ، ولكن فقط كاحتمال. على سبيل المثال ، من الممكن من حيث المبدأ تقسيم الخط إلى عدد لا نهائي من الأجزاء أو الاستمرار في العد الى ما لا نهاية ، ولكن هذا غير ممكن عمليا. لذلك هناك ما لا نهاية المحتملة ، ولكن اللانهاية الحقيقية لا وجود لها. كما قال أرسطو نفسه: "الطبيعة تهرب من اللانهاية لأن اللانهاية غير مكتملة, والطبيعة تبحث دائما عن نهاية".
لا تغادروا اماكنكم.. فما زالت رحلتنا مع اللا نهاية مستمرة في الجزء القادم
حصري لمنتديات درر العراق






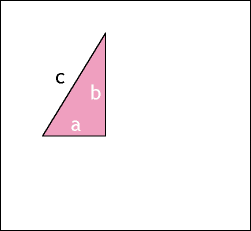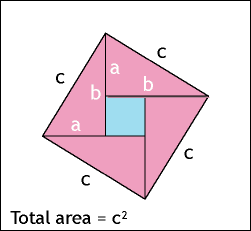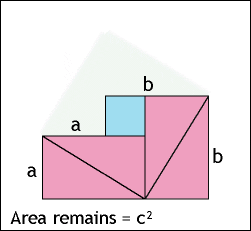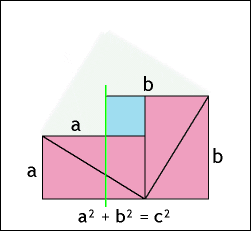
 رد مع اقتباس
رد مع اقتباس